TÍTULO: IMPLEMENTAÇÃO DE UM MODELO COMPUTACIONAL DE GÁS IDEAL MONOATÔMICO UTILIZANDO DINÂMICA MOLECULAR

AUTORES: Silva, J.R. (LCCV/CTEC/UFAL) ; Lira, W.W.M. (LCCV/CTEC/UFAL) ; Cintra, D.T. (LCCV/CTEC/UFAL)

RESUMO:Neste trabalho desenvolve-se um simulador numérico simplificado que utiliza o método de Dinâmica Molecular (DM) para estudar o comportamento termomecânico de um sistema químico de um gás ideal em um espaço bidimensional unitário. A simulação é feita considerando átomos como partículas, o método de integração de Velocity- Verlet e a função potencial de Lennard-Jones para simular os campos de energia e calcular as forças entre os átomos considerando um raio de interação definido. Com o simulador desenvolvido é possível observar características peculiares de um sistema monoatômico, como a influência de temperatura e concentração no movimento dos átomos. Observa-se, ainda, que a função de Lennard-Jones é uma boa escolha para modelagem de sistemas químicos por sua simplicidade.

PALAVRAS CHAVES: Dinâmica Molecular; Potencial deLennard-Jones; Elementos Discretos

INTRODUÇÃO:Em muitas aplicações da engenharia é interessante utilizar meios particulados para resolver problemas complexos de interesse, podendo envolver, por exemplo, o fenômeno de fragmentação. A abordagem pelo Método dos Elementos Discretos (CUNDALL & STRACK, 1979) para esta categoria de problemas é apropriada em virtude de sua natureza inerentemente descontínua. Na engenharia química, o estudo de Dinâmica Molecular para modelagem de sistemas químicos pode ser interessante para interpretar e até prever o comportamento de algum mecanismo interação entre átomos, como o princípio de exclusão de Pauli e as forças de dispersão de van de Waals. O método de Dinâmica Molecular foi proposto inicialmente por (ALDER & WAINWRIGHT, 1959) e é usado para modelar o comportamento de sistemas químicos usando equações de movimento e funções que simulem campos de energia envolvidos na interação entre espécies químicas. A dinâmica do sistema é resolvida de forma discreta ao longo do tempo e a cada passo de integração são atualizadas posições, velocidades e calculadas variáveis de interesse como temperatura e energia. A interação ocorre entre pares de átomos e possui duas características importantes para a simulação: a) resistência à compressão; b) capacidade de manter os átomos unidos nos estados sólido e líquido. Assim, átomos muito próximos se repelem e, a partir de certa distância, se atraem mutuamente. A função de Lennard-Jones é escolhida para a simulação, pois representa bem essas características (RAPAPORT, 2004). Dentro deste contexto, o objetivo deste trabalho é o desenvolvimento de um simulador de Dinâmica Molecular, através do Método dos Elementos Discretos, para observar o comportamento de um gás ideal submetido a diferentes temperaturas e concentrações.

MATERIAL E MÉTODOS:São fornecidas as informações iniciais para a simulação (número de átomos, tempo, distância de interação, passo de integração e temperatura), as posições iniciais são estabelecidas por um parâmetro de rede e as velocidades iniciais são sorteadas por distribuição gaussiana. A função de Lennard-Jones usada para átomos que estão separados por uma distância r, menor que a distância de interação, é dada pela Equação 1. V=q[(s/r)¹²-(s/r)⁶] (1) Nessa equação, q regula a força de interação, s define uma escala de comprimento e r é a distância entre os átomos. Para simplificar equações e evitar problemas do tipo underflow e overflow, adota-se unidades adimensionais, usando m=1, q=1 e r=rs (SABINO et al., 2009). Assim, a função é reescrita: V=q[(1/r)¹²-(1/r)⁶] (2) O cálculo das forças sobre cada átomo é feito com a Equação 3: F=-∇V=12q[(1/r)¹⁴-(1/r)⁸] (3) Para atualizar posições e velocidades usa-se o método de integração de Velocity- Verlet (SCHERER, 2005), o qual utiliza as seguintes equações: s(t+Δt)=s(t)+v(t)Δt+½f(t)Δt² (4) v(t+Δt)=v(t)+½{f(t+Δt)+f(t)}Δt (5) O método é incrementado com um fator de normalização para que o sistema se mantenha a uma temperatura constante Tr. O fator é dado pela Equação 6. vr=√(Tr/((T(t)+T(t+Δt))/2)) (6) E implementado conforme a Equação 7. v=(v-v')vr (7) Onde, v é a componente da velocidade e v' é a média entre as velocidades dos átomos (TRAVIESSO, 1989). Para minimizar a limitação do número de átomos usam-se condições de contorno periódicas, repetindo o espaço de simulação em todas as direções. Energia cinética e temperatura são simuladas usando, respectivamente: E=1/(2N)∑v² (8) t=1/(dn)∑v² (9) sendo, d é a dimensão do modelo (d=2).

RESULTADOS E DISCUSSÃO:O modelo proposto é desenvolvido computacional no ambiente de programação MATLAB, seguindo o esquema da figura 1. É estabelecido um modelo de dimensões unitárias, onde as posições iniciais são definidas por um parâmetro de rede e as velocidades iniciais são escolhidas por sorteio. A cada passo de tempo o algoritmo atualiza posições e velocidades. Em seguida calcula-se a temperatura do sistema e exibe-se a movimentação dos átomos ao lado do gráfico que ilustra a temperatura em função do tempo. É possível visualizar no modelo a interferência da concentração de partículas na simulação. Observa-se na Figura 2 que no modelo (b) existem uma probabilidade maior de encontrar partículas no raio de interação que no modelo (a) e, portanto, a quantidade de forças de interação é alta também. A influência da temperatura no sistema é clara: temperaturas altas ocasionam altas velocidades e baixas temperaturas são responsáveis por velocidades mais baixas. Essa característica da simulação é decorrente da relação entre temperatura e movimento. Em temperaturas elevadas o grau de agitação das partículas é alto. Isto significa que a velocidade das partículas é maior, logo em um sistema de maior temperatura o grau de desordem das partículas é maior, conforme pode ser visto na Figura 2 os modelos (c) e (d).

Figura 1

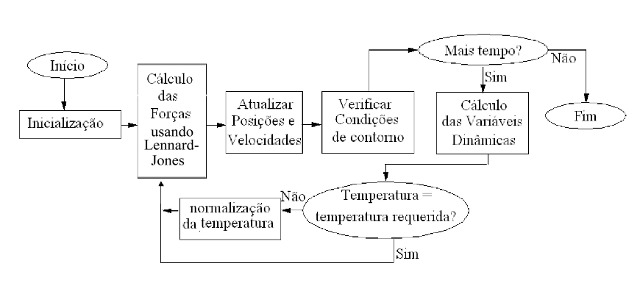
Fluxograma dos passos da simulação de Dinâmica Molecular.

Figura 2

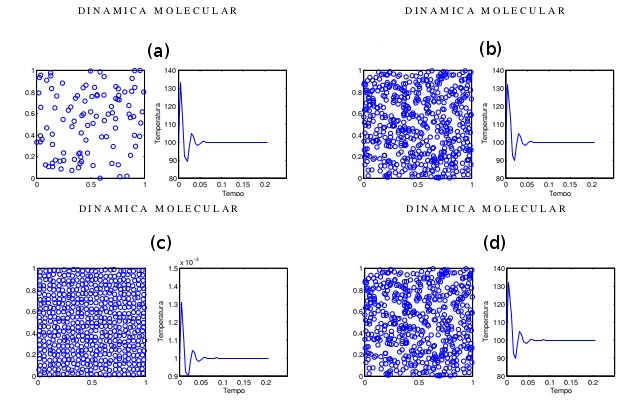
Influência da concentração e a da temperatura no sistema. Em (a) 100 átomos e em (b) 529 átomos. Em (c) o sistema está a 0,001K e em (d) 100K.

CONCLUSÕES:Com o trabalho foi possível concluir que o modelo bidimensional desenvolvido, simulou muito bem um gás ideal, os diferentes parâmetros simulados forneceram resultados satisfatórios, aproximando-se do que seria obtido em um modelo real, onde, de fato, quanto maior a temperatura, maior o movimento entre os átomos e, assim, maior o grau de desordem entre as partículas. Os resultados para o parâmetro que trata da concentração (número de partículas) também se comportaram como esperado, mostrando maior interação quando havia mais partículas no espaço de simulação.

AGRADECIMENTOS:

REFERÊNCIAS BIBLIOGRÁFICA:ALDER, B. J.; WAINWRIGTH, T. E.. Studies in molecular dynamics. i. General method. The Journal of Chemical Physics, vol. 31, n. 2, 1959.

CUNDALL, P. A.; STRACK, O. D. L.. A discrete numerical model for granular assemblies. Geotechnique, 1979.

RAPAPORT, D. C.. The Art of molecular Dynamics Simulation. Cambridge University Press, Second Edition, 565 p., 2004.

SCHERER, C.. Métodos Computacionais da Física. Livraria da Física, 1ª Edição, 284p., 2005.

SABINO, T. L. R.; OLIVEIRA, J. P. S.; PEÇANHA, J. P.; BARROSO, J. S.; ALMEIDA, R. B.; VIEIRA, M. B.; LOBOSCO, M.; DANTAS, S. O.; COLUCI, V. R.. Simulação de Dinâmica Molecular Usando d Potencial de Lennard-Jones. XII Encontro de Modelagem Computacional, Rio de Janeiro, 2009.

TRAVIESO, G.. Estudo de Processamento Paralelo para Dinâmica Molecular. Universidade de São Paulo, São Carlos, 1989.