ÁREA
Química Analítica
Autores
Schmitt, M.A. (ULBRA/CRQ-V/LM) ; Möller, A.C. (ULBRA)
RESUMO
Uma empresa privada do ramo petroquímico possui duas unidades que operam com a tecnologia Spherilene para produção de polietileno, porém as etapas de reação possuem frequência de coleta para a análise da densidade diferente. O objetivo foi avaliar a possibilidade da unificação da frequência com base no estudo estatístico dos resultados obtidos em campanhas passadas. Através da avaliação dos modelos, do histórico de produtos fora de especificação e das principais características das plantas, foi possível concluir que a redução na frequência analítica é possível para a maioria dos produtos da unidade Alfa, bem como a unificação da frequência de análise de densidade dos reatores. Para a unidade Beta apenas metade das avaliações foi favorável à redução.
Palavras Chaves
polietileno; controle de qualidade; ARIMA
Introdução
Uma empresa privada de segunda geração petroquímica do Estado do Rio Grande do Sul, que possui 12 plantas industriais mais plantas piloto, é atendida por um laboratório de controle de qualidade que está passando por um processo de unificação. Antes atendidas por laboratórios diferentes, e agora pelo mesmo laboratório de polímeros, duas das plantas de segunda geração petroquímicas utilizam a mesma tecnologia de produção de polietileno que é Spherilene. A principal característica do processo do tipo Spherilene é a utilização de dois reatores fase gás em série, e é principalmente utilizado para a produção de polietileno de baixa densidade, ou seja, com a adição de comonômeros (GAMBETTA, 2001). O catalisador utilizado é do tipo Ziegler-Natta heterogêneo e é alimentado no reator de pré-polimerização (FLORES, 2006). O monômero, neste caso o eteno, é inserido no primeiro reator do tipo Bulk de forma fluidizada. Após passar pelo segundo reator do mesmo tipo, o polímero sofre um processo de retirada do monômero restante e desativação do catalisador. O polímero úmido é obtido em esferas, é secado com nitrogênio e então encaminhado para aditivação e extrusão em pellets (FLORES, 2006). As etapas deste processo que são analisadas para controle de qualidade da resina e processo são as esferas do primeiro e segundo reator, e os pellets na etapa de granulação. O polietileno granulado é enviado para um silo, onde sofre um processo de homogenização. O conjunto de material homogêneo em um silo é denominado lote. Apesar de todas as resinas produzidas nas unidades Spherilene serem polietileno elas possuem algumas diferenças como tipo e quantidade de aditivos dosados ou comonômeros, que variam conforme a aplicação desejada para cada produto. Cada receita diferente é denominada grade, e um mesmo grade será sempre produzido seguindo as mesmas especificações. Cada conjunto de lotes produzidos sequencialmente de um mesmo grade é denominado campanha. Dentre as principais propriedades do polietileno (PE) as que normalmente são monitoradas durante a sua produção nas unidades industriais são a densidade e o índice de fluidez (IF) (GAMBETTA, 2001). Para determinação da densidade da resina, as principais técnicas que são utilizadas são as de determinação via coluna gradiente, conforme a norma ASTM D1505 (2018), e via deslocamento de líquidos, que segue a norma ASTM D792 (2020). No laboratório em que o projeto foi desenvolvido, a densidade das resinas PEBD e PEBDL são realizadas através do método de coluna gradiente, enquanto a densidade dos polímeros PEAD pode ser determinada tanto pelo método gradiente quanto pelo método de deslocamento de líquido. A determinação de qual metodologia utilizar para determinação do parâmetro é da engenharia de processo responsável pela unidade industrial. Com relação à periodicidade, o que dita a frequência com que as análises serão realizadas em cada etapa do processo é um documento de comunicação interna da empresa denominado plano de análises, que é elaborado pelo laboratório em conjunto com a engenharia de produção da planta. A frequência de análise de densidade é a mesma nas duas plantas para granulação e produto final, porém é significativamente diferente para as amostras de reatores, o que gera conflito nos horários de amostragem e desencontro nas atividades do analista. Sendo assim, com a unificação dos laboratórios e tendo duas plantas que operam com o mesmo tipo de processo, este trabalho teve por finalidade estudar a possibilidade de unificação da frequência de análises de densidade dessas dos reatores para produtos que são analisados via coluna gradiente nas duas unidades das unidades que utilizam a tecnologia Spherilene para produção de polietileno. Para esta avaliação foi realizada uma análise estatística do histórico de análises, utilizando a metodologia ARIMA de previsão de séries temporais. Uma série temporal pode ser definida como um conjunto de dados observados ao longo de um período no tempo, como resultados de análise de controle de qualidade de processo emitidos em intervalos fixos e pré-definidos. De acordo com Campos, Clemente e Cordeiro (2006) o modelo ARIMA (Auto Regressivo Integrado de Média Móvel) é próprio para previsões de séries temporais. Os modelos autorregressivos baseiam-se na ideia de que o valor atual de uma série de dados X, pode ser explicado como uma função de p valores passados, onde p determina o número de etapas no passado necessárias para prever o valor atual (COSTA NETO, 2002). Caso o modelo indique a viabilidade de redução da frequência analítica, o trabalho irá propor intervalos de análises unificados visando a otimização de recursos do laboratório de polímeros sem prejuízo à qualidade do produto final e ao processo produtivo.
Material e métodos
Primeiramente foi realizado o levantamento do histórico de análises de densidade e o período escolhido foi de 3 anos, período em que se obteve quantidade expressiva e representativa de dados, além de variedade de especificações de produto diferentes. Os dados extraídos do sistema da empresa foram exportados para Microsoft Excel, e separados por grade, por etapa do processo e por campanha de produção. Após a organização dos dados do histórico, foram aplicadas as ferramentas previstas. O conjunto de resultados de densidade da etapa de reação, por planta, por grade e por campanha foram submetidos ao modelo ARIMA (Auto Regressivo Integrado de Média Móvel), em software estatístico Minitab, a ferramenta computacional escolhida para suporte à aplicação do modelo. Foram testadas algumas combinações de fatores Autoregressivo, Diferencial e Média Móvel do modelo ARIMA. Para cada conjunto de dados, a combinação dos parâmetros que gera o melhor modelo pode ser diferente, portanto os testes devem ser realizados para cada produto e ponto de análise (primeiro e segundo reator), em cada uma das plantas. A partir dos vários modelos gerados, foi selecionado aquele que mais se adequou ao conjunto de dados para ser avaliado neste trabalho. Para esta avaliação, primeiramente foi realizada a comparação do valor-p obtido para os termos do modelo com relação à significância, a fim de garantir que o termo não seja significativamente diferente de 0. Se o valor de p for menor ou igual ao nível de significância, é possível concluir que o coeficiente é estatisticamente significativo e portanto o termo pode ser mantido no modelo, ou que foi corretamente aplicado. O nível de significância utilizado foi de 0,05, que é o valor padrão adotado em modelos no programa e indica um risco de 5% de concluir que o termo não é significativamente diferente de 0 quando for significativamente diferente de 0. Em seguida foi determinado se o modelo atende à suposição da análise, através do uso da estatística de qui-quadrado de Ljung-Box e da função de autocorrelação dos resíduos. Estes recursos são utilizados para determinar se o modelo satisfaz aos pressupostos de que os resíduos são independentes e que, caso não seja atendida, indica que o modelo pode não se ajustar aos dados. Para esta avaliação, é realizada a comparação do valor de p deste cálculo com o nível de significância para cada estatística Qui-Quadrado. O nível de significância aplicado nesta análise foi o mesmo que o utilizado nas etapas anteriores. Se o valor de p for maior do que o nível de significância é possível concluir que os resíduos são independentes e que o modelo atende à suposição. Já através do gráfico gerado de função de autocorrelação dos resíduos (FAC), é avaliado se existem correlações significativas presentes, ou seja, que ultrapassem o limite de significância no gráfico. Caso todas as correlações estejam dentro do nível de significância, é possível concluir que os resíduos são independentes.
Resultado e discussão
Para a análise estatística foram modelados 3 conjuntos de dados separados por
reator de cada planta e por grade, sendo selecionados aqueles que possuíam maior
quantidade de dados. Foram realizados testes de modelagem com diferentes
combinações de parâmetros e, dos conjuntos de parâmetros testados no modelo, foi
escolhido aquele que melhor se adequou ao grupo de dados com base nos parâmetros
citados no capítulo anterior.
Interpretação dos resultados
O resultado obtido da modelagem ARIMA é um gráfico de predição de valores
futuros da característica em análise com base no histórico fornecido. Os valores
obtidos foram avaliados de maneira a determinar em quantos valores futuros, na
frequência de análises atual, o resultado estará fora da especificação do
produto. Caso o primeiro valor modelado já esteja fora da especificação,
significa que a análise não pode ser espaçada pois o processo depende dessa
análise e correção constante. Já se o primeiro resultado fora de especificação
fosse o quinto dado modelado, significaria que a análise de densidade poderia
ser espaçada em até quatro intervalos de tempo para esta etapa do processo, sem
comprometer a qualidade do processo e do produto final.
A seguir estão exemplos do método ARIMA obtido das etapas de produção do grade
LL118/21 nas duas unidades industriais.
Nos gráficos os pontos azuis se referem aos resultados reais de densidade
emitidos para a campanha, enquanto os pontos vermelhos se referem aos resultados
futuros previstos pelo modelo. Os pontilhados em vermelho indicam os valores de
especificação inferior e superior de densidade da resina para esta etapa do
processo.
Os resultados de modelagem vistas nos gráficos A e C da Figura 1 indicam
tendência de produção dentro da especificação do produto, enquanto o modelo
visto no gráfico B prevê que apenas o primeiro resultado futuro estará fora da
especificação, enquanto que os seguintes já estariam dentro da especificação
novamente. Além disso, o modelo para a terceira campanha apresentou valor-p
acima dos padrões de qualidade do trabalho, o que indica que alguns dos termos
pode não ter sido corretamente aplicado e portanto o modelo pode não se adequar
perfeitamente à série. Tendo os modelos válidos apresentado resultados futuros
dentro da especificação do produto, conclui-se que a frequência de análise para
este produto e etapa do processo pode ser reduzida sem prejuízo ao processo ou
produto final.
Com base na avaliação gráfica ARIMA foi possível concluir sobre reator unidade
alfa e unidade beta.
Considerações e resumo da avaliação estatística
Uma das limitações identificadas neste trabalho é para os casos de conjuntos de
dados em que os resultados da campanha já estão fora de especificação,
encontrados principalmente no ponto de primeiro reator. Além disso, para essa
mesma campanha, os resultados de segundo reator estão dentro da especificação. É
o caso dos produtos LH118, LH0820/21AF, HE150 e LL4405S, em que foi sugerida uma
avaliação complementar da quantidade de produto fora de especificação gerado no
período do levantamento de dados, a fim de auxiliar na avaliação da
possibilidade de redução da frequência analítica. Ao todo foram encontrados 10
lotes com densidade fora de especificação.
Para os grades LH118 e LH0820/21AF não há lotes de produto final com densidade
fora de especificação, portanto considera-se que a frequência das análises de
densidade no primeiro reator destes produtos pode ser reduzida sem prejudicar a
qualidade do produto final.
Já para o produto HE150, a quantidade total produzida no período de análise foi
de 375 lotes, quatro destes fora de especificação para densidade que representam
apenas 1,1% de produto off-spec. Por ser uma parcela muito pequena dos lotes
produzidos, pode-se assumir que os resultados fora de especificação no primeiro
reator para este produto não refletem em maior quantidade de produto final fora
de especificação. Da mesma forma para o produto LL4405S, em que foram
identificados 115 lotes de produto final no período de seleção dos dados e dois
lotes fora de especificação para densidade, que correspondem a apenas 1,7% de
produto off-spec. Portanto, para este produto também é possível concluir que os
resultados fora de especificação no primeiro reator não refletem em maior
quantidade de resultados fora de especificação tanto no segundo reator quanto
nos lotes de produto final.
O comparativo entre as plantas mostra que a unidade Alfa, que hoje possui maior
frequência de análises, também possui maior capacidade produtiva. Esta unidade
também produz lotes maiores do que a unidade Beta, portanto ao mesmo tempo que
uma oscilações no processo não identificadas pela análise de laboratório, essa
oscilação é mais diluída no lote de produto final que está sendo formado.
Além disso a avaliação estatística indicou que para a maioria dos
produtos avaliados é possível reduzir a frequência de análise na unidade Alfa
sem prejudicar a qualidade ou quantidade de produto fora de especificação
gerado. Também não há registro de reclamações de cliente por desvio de qualidade
na densidade da resina.
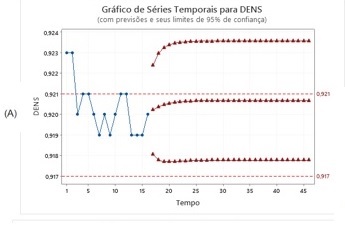
Gráficos ARIMA de LL118/21 para 1º reator da planta \r\nAlfa
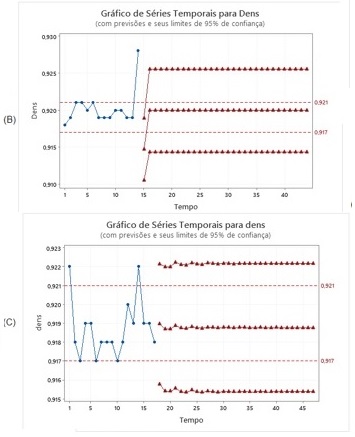
Gráficos ARIMA de LL118/21 para 1º reator da planta \r\nAlfa
Conclusões
Através do estudo do histórico de análises de densidade das duas unidades Spherilene estudadas, com a aplicação da modelagem ARIMA, avaliação da quantidade de produto fora de especificação e principais características das plantas, foi possível concluir que a redução da frequência analítica é possível para a maioria dos produtos na unidade Alfa, bem como a unificação da frequência de análise de densidade dos reatores das plantas. A modelagem ARIMA foi aplicada para indicar se a frequência de análises de densidade poderia ser reduzida sem que se gerasse maior quantidade de produto fora de especificação durante as campanhas de produção. Os produtos submetidos à modelagem ARIMA foram aqueles analisados via método ASTM D1505, e que são comuns às duas unidades. Foram realizadas análises dos dados separados por grade, etapa do processo e campanha de produção em programa estatístico, e depois avaliados os parâmetros de qualidade dos modelos e gráficos gerados. Dos sete produtos e 14 etapas de processo avaliados para a unidade Alfa, a análise estatística foi positiva à redução das análises para 10, representando 71%, e com a avaliação complementar de produto fora de especificação gerado, 5 dos grades avaliados foram aprovados nas duas etapas do proceso. Já para a unidade Beta a modelagem ARIMA foi favorável à redução para apenas três das oito das etapas avaliadas, o que representa 37,5%, e nenhum produto foi aprovado nas duas etapas. Esses resultados estão em concordância com a freqüência atual de análises nas duas unidades, em que a unidade Beta já possui menor freqüência de análises. A principal dificuldade encontrada no estudo foi com relação às campanhas de produção curtas, ou ainda conjuntos com resultados muito dispersos, que resultam em séries com poucos dados e dificultam a adequação do modelo.
Agradecimentos
CONSELHO REGIONAL DE QUÍMICA - QUINTA REGIÃO - CRQ-V UNIVERSIDADE LUTERANA DO BRASIL - ULBRA CAMPUS CANOAS/RS LEARN WITH MAURÍCIO SCHMITT - LM
Referências
ABIPLAST - ASSOCIAÇÃO BRASILEIRA DA INDÚSTRIA DO PLÁSTICO (2018a). Perfil 2017. Publicação anual da ABIPLAST. Disponível em: <http://file.abiplast.org.br/file/download/2018/Perfil_WEB.pdf>. Acesso em: 11 nov. 2022.
AKCELRUD, L. Fundamentos da Ciência dos Polímeros. Editora Manole Ltda, São Paulo, 2007.
AMERICAN SOCIETY FOR TESTING AND MATERIALS. ASTM D792: Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement. West Conshohocken, 2020.
_____. ASTM D1505: Standard Test Method for Density of Plastics by the Density-Gradient Technique. West Conshohocken, 2018.
CAMPOS, Paulo André Cavalcanti; CLEMENTE, Ademir; CORDEIRO, Agnaldo Antônio Lopes de. Aplicação Do Modelo Arima Para Previsão Do Preço Do Frango Inteiro Resfriado No Grande Atacado Do Estado De São Paulo. XIII Congresso Brasileiro De Custos: 2006, Belo Horizonte. p. 1-16.
CANEVAROLO Jr, Sebastião. Ciência dos Polímeros. Artiliber Editora Ltda, São Carlos, 2004.
CARVALHO, José Luiz M.; TOLEDO, José Carlos de. Restruturação produtiva, programas da qualidade e certificações ISO 9000 e ISO 14000 em empresas brasileiras: pesquisa no setor químico/petroquímico. Polímeros: Ciência e Tecnologia, São Carlos, v. 10, n. 4, p. 179-192, nov. 2000. Disponível em: <https://www.scielo.br/j/po/a/qpn59x7bP5XPdLYpQMsXm5M/?lang=pt&format=pdf>. Acesso em: 06 set 2022.
COSTA NETO, Pedro Luiz de Oliveira. Estatística. 2. ed. São Paulo: Edgard Blucher Ltda, 2002.
COUTINHO, F. M. B.; MELLO, I. L.; SANTA MARIA, L. C. Polietileno: Principais Tipos, Propriedades e Aplicações. Instituto de Química, UERJ, 2003. Disponível em: <https://www.scielo.br/j/po/a/vzPmcF9tLYGRPvK67CnWj9S/?lang=pt&format=pdf> Acesso em 25 ago. 2022.
CRQ4. Petroquímica. Disponível em: <https://www.crq4.org.br/default.php?p=texto.php&c=quimica_viva__petroquimica.> Acesso em 31 de agosto de 2022.
EPE - EMPRESA DE PESQUISA ENERGÉTICA. Ministério de Minas e Energia. Nota Técnica DPG-SPT Nº 04/2018: panorama do refino e da petroquímica no brasil. Rio de Janeiro, 2018. Disponível em: <https://www.epe.gov.br/sites-pt/publicacoes-dados-abertos/publicacoes/PublicacoesArquivos/publicacao-/topico-412/NT%20Refino%20e%20Petroqu%C3%ADmica_2018.11.01.pdf>. Acesso em: 11 nov. 2022.
FAVA, Vera Lúcia. Análise de séries de tempo. In: VASCONSELOS, M. A. S.; ALVES, Denisard (Org.). Manual de Econometria: nível intermediário. São Paulo: Atlas, 2000a. p. 199-203.
______. Metodologia de Box-Jenkins para modelos univariados. In: VASCONSELOS, M. A. S.; ALVES, Denisard (Org.). Manual de Econometria: nível intermediário. São Paulo: Atlas, 2000b. p. 205-231.
______. Teste de raízes unitárias e co-integração. In: VASCONSELOS, M. A. S.; ALVES, Denisard (Org.). Manual de Econometria: nível intermediário. São Paulo: Atlas, 2000c. p. 233-243.
______. Modelos de função de transferência e de análise de intervenção. In: VASCONSELOS, M. A. S.; ALVES, Denisard (Org.). Manual de Econometria: nível intermediário. São Paulo: Atlas, 2000d. p. 244-252.
FLORES, Tanise Mori. Modelagem da Copolimerização de Olefinas: Estudo da Aplicabilidade de Dados em Fase Líquida para a Fase Gás. 2006. 190 f. Dissertação (Mestrado) - Curso de Engenharia Química, Departamento de Engenharia Química, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2006. Disponível em: <https://www.lume.ufrgs.br/bitstream/handle/10183/11799/000612805.pdf?sequence=1&isAllowed=y>. Acesso em: 06 set. 2022.
GAMBETTA, Rossano. Modelagem e Simulação de Reatores de Polimerização em Leito Fluidizado. 2001. 138 f. Dissertação (Mestrado) - Curso de Engenharia Química, Departamento de Engenharia Química, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2001. Disponível em: <https://www.lume.ufrgs.br/bitstream/handle/10183/3162/000333228.pdf?sequence=1&isAllowed=y>. Acesso em: 06 set. 2022.
MANO, E. B.; MENDES, L. C. Introdução a polímeros. 2. ed. São Paulo: Edgard Blücher, 1985. 191p.
MINITAB STATISTICAL SOFTWARE. Suporte ao Minitab 20. Exemplo de ARIMA. Disponível em: <https://support.minitab.com/pt-br/minitab/20/help-and-how-to/statistical-modeling/time-series/how-to/arima/before-you-start/example/>. Acesso em: 11 mar. 2023.
MINITAB STATISTICAL SOFTWARE. Suporte ao Minitab 21. Interprete os principais resultados para Previsão com o melhor modelo ARIMA. Disponível em: <https://support.minitab.com/pt-br/minitab/21/help-and-how-to/statistical-modeling/time-series/how-to/forecast-with-best-arima-model/interpret-the-results/key-results/>. Acesso em: 17 abr. 2023.
SHACKELFORD, J. F. Ciências dos Materiais. 6° ed. São Paulo: Pearson Education, 2008.
SPIEGEL, Murray R.; STEPHENS, Larry J.. Estatística: coleção schaum. 4. ed. São Paulo: Bookman Companhia Editora, 2009.
QUIRINO, Poliana Pastorele da Silva. Estratégias de controle aplicadas a reatores de polimerização de eteno em solução. 2012. 166 f. Dissertação (Mestrado) - Curso de Engenharia Industrial, Ufba, Salvador, 2013. Disponível em: <https://repositorio.ufba.br/handle/ri/14050>. Acesso em: 06 set. 2022.