Autores
Cosmo, P.H.A. (INSTITUTO DE QUÍMICA - UNICAMP) ; Custodio, R. (INSTITUTO DE QUÍMICA - UNICAMP)
Resumo
No presente trabalho avaliou-se o desempenho de métodos de extrapolação
empregando diferentes expressões matemáticas utilizadas na literatura para a
previsão de entalpias de formação para o conjunto de base completo empregando a
teoria do funcional de densidade. As entalpias de formação foram calculadas com
o programa Gaussian09 para um conjunto de 250 moléculas em nível B3LYP
com conjuntos de base aug-cc-pVNZ (em que, N = D, T e Q). Para a
otimização dos parâmetros de extrapolação foi utilizado o algoritmo
Simplex de Nelder e Mead nas expressões empregadas com o auxílio
de um roteiro computacional em linguagem Python. Dentre as expressões
desenvolvidas a que produziu o melhor desempenho diminuiu em 77,8% o erro
quadrático médio e em 71% o erro absoluto médio.
Palavras chaves
Métodos de Extrapolação; Entalpia de Formação; Funcional de Densidade
Introdução
A química computacional pode ser usada para estimar propriedades
termoquímicas rigorosamente para uma ampla variedade de sistemas. A teoria do
funcional da densidade (DFT) é uma das alternativas, sendo bem aceita e
amplamente disponível em diversos softwares para calcular propriedades de
átomos, moléculas e sólidos. Enquanto os métodos tradicionais de estrutura
eletrônica de alto nível exigem um esforço computacional crescente com o aumento
do número de elétrons, a DFT propõe uma abordagem mais simples utilizando a
função densidade, n(r) (KURTH; MARQUES; GROSS, 2005).
Dois dos aspectos mais importantes na resolução de problemas de estrutura
eletrônica são o de correlação eletrônica e a escolha apropriada das
funções de base. A introdução de métodos de extrapolação para o
Conjunto de Base Completo (CBS) de correlação-consistente dos
conjuntos de base produzidos por Dunning em 1989 (DUNNING, 1989), cc-
pVnZ, em que: n = D, T, Q, 5, 6 etc., levou a uma mudança nas
estratégias para soluções rigorosas da equação Schrödinger. Usando
sequências desses conjuntos de base com um método de estrutura eletrônica, pode-
se estimar a partir de uma extrapolação o limite CBS, eliminando-se assim o
problema da incompletude do conjunto de base e a utilização de conjuntos de
funções de base extensas, que seriam de difícil resolução computacional. Além
disso, problemas com erros de superposição de base são minimizados (DIXON;
FELLER; PETERSON, 2012). Além da estratégia de extrapolação com conjuntos de
base, existem ainda estratégias como a dos métodos de otimização para a
minimização dos erros de um conjunto de valores a partir de uma expressão
matemática com parâmetros ajustáveis. Uma estratégia bastante utilizada para
encontrar os parâmetros ótimos da diminuição de erros em expressões matemáticas
é a utilização de roteiros computacionais de minimização. Nelder e Mead (NELDER;
MEAD, 1965) descreveram um método onde o algoritmo simplex adapta-se ao
espaço gerado pelos dados em um processo dinâmico, em que os parâmetros são
selecionados de forma não-linear contraindo o sistema a uma região de mínimo.
Gao e Han (GAO; HAN, 2012) mencionam ainda que este método é amplamente
utilizado por exigir um baixo esforço computacional.
O objetivo do presente trabalho é minimizar os erros de entalpias de formação
molecular (EFM) calculadas em relação aos valores experimentais a partir de
equações de extrapolação para funções de base completas (JENSEN, 2005), (KARTON;
MARTIN, 2006) e (VARANDAS, 2007) empregando a teoria do funcional de densidade.
Material e métodos
Os cálculos de átomos e moléculas para a obtenção das entalpias de formação
foram calculados com o auxílio do programa Gaussian09 (FRISCH et al.,
2013). As entalpias foram calculadas para um conjunto de 250 moléculas (PEREIRA
et al., 2011) utilizando o funcional B3LYP e conjuntos de funções de base
aug-cc-pVNZ, em que N = D, T e Q. O procedimento para o cálculo
das entalpias de formação e parte dos dados termoquímicos está detalhadado no
texto “Thermochemistry in Gaussian” de Joseph Ochterski (OCHTERSKI,
2000). Com os valores das entalpias de formação de cada molécula, minimizou-se a
diferença entre os valores calculados e o experimental, a partir do
desenvolvimento de expressões com parâmetros ajustáveis. Os parâmetros foram
selecionados com o auxílio de um roteiro computacional na linguagem
Python (ROSSUM, 2022) utilizando o método Simplex de Nelder-
Mead. Para a construção das expressões de minimização foram utilizadas
equações de extrapolação descritas pela literatura. As equações utilizadas, bem
como, a metodologia de construção das expressões de minimização está na Tabela
1.
Para construção das equações de minimização dos erros foi realizado um rearranjo
nas equações de E1 a E7 de acordo com o exemplificado para a equação E1 nas
expressões R1Q e R1A. Como pode ser observado, foi construído um somatório das
diferenças entre as entalpias calculadas com os diferentes conjuntos de função
de base e a entalpia experimental, ponderado por termos com parâmetros
ajustáveis. O desempenho das equações foi avaliado com a minimização das
diferenças ao quadrado e em absoluto, como também foi exemplificado para E1 em
R1Q e R1A, respectivamente.
Resultado e discussão
O comportamento das Eqs. de E1 a E7 foi analisado a partir do desempenho com o
rearranjo R1Q e os resultados produzidos pelas expressões estão apresentados na
Figura 1(a). Observa-se que as Eqs. E4 e E7 foram as que produziram,
respectivamente, o menor e o maior valor para o erro dentre as equações
estudadas. As Eqs. E1, E3, E5 e E6 produziram resultados próximos entre si.
Nota-se também que todas as equações produziram um desempenho melhor do que a
expressão do EQM sem nenhum parâmetro ajustável. A Eq. E4 apresentou uma
diminuição de 155,41 kcal.mol-1 no erro médio, representando uma
melhora de 77,8%. As Eqs. E1, E3, E5 e E6 que produziram resultados próximos
entre si, apresentaram uma diminuição média de 83,37 kcal.mol-1,
melhorando em cerca de 41,7% as entalpias calculadas em relação aos cálculos sem
utilizar qualquer extrapolação. A Eq. E7 apresentou uma diminuição de 34,75
kcal.mol-1 no valor do erro médio, o que representa uma melhora de
17,4%. Pode-se destacar também, que o desempenho apresentado pelas Eqs. E1, E2,
E3 e E4, com parâmetros ótimos das extrapolações do tipo exponencial produziram
um valor médio de 105,9 kcal.mol-1 e que as Eqs. E5, E6 e E7 com
otimização de equações do tipo potencial produziram um desvio médio de 133,41
kcal.mol-1. Isso representa uma melhora de 47% produzido pelas
equações exponenciais e 33,7% pelas equações potenciais nos valores do EQM do
conjunto de moléculas.
O comportamento das Eqs. de E1 a E7 também foi analisado a partir do desempenho
com o rearranjo R1A e os resultados produzidos são mostrados na Figura 1(b).
Observa-se que as Eqs. E1, E2, E3, E5 e E6 produziram resultados próximos entre
si e o menor e maior erro médio foram produzidos, respectivamente, pelas Eqs. E4
e E7. A diminuição do erro produzido pelas Eqs. E1, E2, E3, E5 e E6 foi de cerca
de 1,53 kcal.mol-1, o que representa uma melhora de 16,2% produzido
por estas expressões em comparação com a equação de EAM sem nenhum termo de
otimização. A diminuição do erro produzida pela Eq. E7 foi de 0,75
kcal.mol-1, o que representa um melhor desempenho de 7,9% em
comparação com a equação de EAM. A diminuição do erro produzido pela Eq. E4 foi
de 6,7 kcal.mol-1, o que representa uma melhora de 71% no erro médio
das moléculas em comparação com a equação de EAM. Destaca-se também que as Eqs.
E1, E2, E3 e E4, com termos da minimização das diferenças do tipo exponencial,
produziram uma diminuição média do erro de 2,84 kcal.mol-1, o que
representa uma melhora média de 30% no valor do erro das moléculas. As Eqs. E5,
E6 e E7, com termos da minimização das diferenças do tipo potencial, produziram
uma diminuição média do erro de 8,21 kcal.mol-1, o que representa uma
diminuição média de 13% no erro médio das moléculas em comparação com a equação
de EAM sem nenhum termo de minimização dos erros.
Os valores produzidos neste trabalho para o EQM e o EAM foram, respectivamente,
199,87 e 9,45 kcal.mol-1. A Eq. E4 foi a que produziu a melhor
desempenho na diminuição das diferenças do conjunto de moléculas estudadas
produzindo, respectivamente, para os métodos R1Q e R1A, os valores de 44,46 e
2,8 kcal.mol-1. Duan et. al. (DUAN et al., 2004) avaliaram a EFM de
um conjunto de 180 moléculas orgânicas de tamanho pequeno e médio em nível
B3LYP/6-311+G(d,p). Para o nível citado os autores produziram um EQM de 457
kcal.mol-1 e um EAM de 18,9 kcal.mol-1. Após aplicação de
um algoritmo de regressão linear proposto no trabalho para o cálculo da EFM, os
valores de EQM e EAM passaram a 3,1 e 2,4 kcal.mol-1,
respectivamente. Shafagh, Hughes e Pourkashanian (SHAFAGH; HUGHES;
POURKASHANIAN, 2011) calcularam a entalpia de formação para um conjunto de 50
hidrocarbonetos com o nível B3LYP/6-311G(d,p). Para o nível citado os autores
produziram um EAM de 35,19 kcal.mol-1. Após aplicação de uma correção
na energia de atomização proposta no trabalho para o cálculo da EFM, o valor do
EAM passou para 5,1 kcal.mol-1. Duan et. al. (DUAN et al., 2005)
estimaram o valor da entalpia de formação para 180 moléculas orgânicas com o
nível B3LYP/6-311G(2d,d,p). Para o nível citado os autores produziram um EQM de
231 kcal.mol-1 e um EAM de 12,4 kcal.mol-1. Após aplicação
de um algoritmo de regressão linear proposto no trabalho para o cálculo da EFM,
os valores de EQM e EAM passaram a 12,25 e 2,3 kcal.mol-1,
respectivamente. Através da literatura citada, observa-se que os resultados
deste trabalho para o EQM e o EAM estão com desvios próximos, porém, menores do
que os citados. Parte dessa diminuição relativa nos valores encontrados pode
estar relacionado ao conjunto de base utilizado ser maior do que o utilizado
pela literatura citada (LEE et al., 2005). Os valores produzidos pelos métodos
citados em (DUAN et al., 2004) e (DUAN et al., 2005) são menores do que os
produzidos pelos métodos estudados neste trabalho, porém, observa-se que o
conjunto de moléculas tratadas pelos autores citados é notavelmente menor do que
o estudado neste trabalho, ademais, os autores estudaram moléculas com menor
diversidade nas características estruturais. Estruturas semelhantes em um
conjunto de moléculas, pode tornar os desvios próximos em relação aos valores de
referência, tornando mais provável um parâmetro que minimize melhor os erros do
conjunto. Muitos trabalhos encontrados na literatura realiza o estudo de grupos
moleculares com características estruturais semelhantes como, por exemplo:
cianos derivados (LI et al., 2010b); furanos derivados (LI et al., 2010a), nitro
ésteres (LI et al., 2009) e complexos metálicos (NAKAJIMA; SEINO; NAKAI, 2017).
Uma forma de ter maior clareza sobre a qualidade dos resultados produzidos pelo
método de minimização proposto neste trabalho, é confrontar o resultado com o
produzido por métodos de alta eficiência. El-Nahas, El-Demerdash e Meshhal
(MESHHAL; EL-DEMERDASH; EL-NAHAS, 2019) utilizaram o método CBS-QB3 para
calcular a EFM de um conjunto de 34 compostos orgânicos aromáticos e
heteroaromáticos. O valor do EAM em relação ao valor experimental produzido pelo
grupo foi 1,06 kcal.mol-1. Denis (DENIS, 2003) utilizou o método
CCSD(T)/aug-cc-pV(T+D)Z para calcular a EFM para um conjunto de 12 moléculas
compostas por átomos de enxofre. O valor do EAM em relação ao valor experimental
produzido pelo autor foi de 8,22 kcal.mol-1. Wilson, Lucente-Schultz
e Prascher (PRASCHER; LUCENTE-SCHULTZ; WILSON, 2009) utilizaram os métodos
CCSD(T) e ccCA com conjunto de base CBS(DTQ5) para calcular a EFM de um conjunto
de 24 moléculas constituídas por SinHXm-n em que X= F, Cl, n = 0 até m, e m = 1
até 4. O valor do EAM em relação ao valor experimental produzido pelo autor foi
de 1,75 kcal.mol-1. Como pode ser analisado pela literatura, métodos
de alta eficiência para conjuntos menores de moléculas com composição estrutural
próximas e constituídas por átomos semelhantes produziram, em média, um EAM de
3,67 kcal.mol-1. Dessa maneira, pode-se considerar que o valor
produzido pelo método proposto neste trabalho, do tipo R1A da Eq. E4 para um
conjunto de 250 moléculas com estruturas não relacionadas, é razoável. Isso,
porque, embora o resultado não tenha sido tão preciso quanto o produzido por
métodos de alta eficiência como citado na literatura investigada, o custo
computacional para o cálculo da EFM de 250 moléculas com métodos de alta
eficiência seria muito maior.

Equações utilizadas para construir as expressões de minimização dos erros.
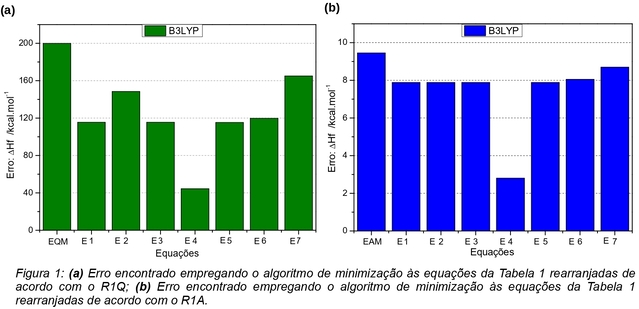
Desempenho das equações rearranjadas de acordo com o (a) R1Q e (b) R1A.
Conclusões
O método proposto produziu o melhor desempenho com a Eq. E4 no R1Q com uma melhora
de 77,8% do erro nas entalpias de formação calculadas em relação aos mesmos
valores sem nenhum ajuste quando comparados com valores experimentais. O menor
valor para o erro médio foi alcançado com a Eq. E4 no R1A com um valor de 2,8
kcal/mol para o conjunto de 250 moléculas. Os resultados produzidos
indicam ainda, que o melhor método para se otimizar as equações foi o R1A.
Agradecimentos
Os autores agradecem a bolsa recebida por Cosmo P.H.A. através da CAPES. A FAPESP
Concessão 2013/08293-7. Ao FAEPEX-UNICAMP. Ao CENAPAD-SP e ao CEPID.
Referências
CHAI, T.; DRAXLER, R. R. Root mean square error (RMSE) or mean absolute error (MAE)? -Arguments against avoiding RMSE in the literature. Geoscientific Model Development, v. 7, n. 3, p. 1247–1250, 2014.
DENIS, P. A. High order correlation effects in the calculation of enthalpies of formation of sulfur compounds, CCSDT vs CCSD[T]. Chemical Physics Letters, v. 382, n. 1–2, p. 65–70, 2003.
DIXON, D. A.; FELLER, D.; PETERSON, K. A. A Practical Guide to Reliable First Principles Computational Thermochemistry Predictions Across the Periodic Table. [s.l.] Elsevier, 2012. v. 8
DUAN, X. M. et al. Accurate prediction of heat of formation by combining Hartree-Fock/density functional theory calculation with linear regression correction approach. Journal of Chemical Physics, v. 121, n. 15, p. 7086–7095, 2004.
DUAN, X. M. et al. Neural network correction for heats of formation with a larger experimental training set and new descriptors. Chemical Physics Letters, v. 410, n. 1–3, p. 125–130, 2005.
DUNNING, T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. The Journal of Chemical Physics, v. 90, n. 2, p. 1007–1023, 1989.
FELLER, D. et al. On the effectiveness of CCSD ( T ) complete basis set extrapolations for atomization energies On the effectiveness of CCSD ( T ) complete basis set extrapolations for atomization energies. v. 044102, 2011.
FRISCH, M. J. et al. Gaussian 09Wallingford CTGaussian, Incorporated, , 2013. Disponível em: <https://gaussian.com/>
GAO, F.; HAN, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Computational Optimization and Applications, v. 51, n. 1, p. 259–277, 4 jan. 2012.
JENSEN, F. Estimating the Hartree — Fock limit from finite basis set calculations. p. 267–273, 2005.
KARTON, A.; MARTIN, J. M. L. Comment on : “ Estimating the Hartree – Fock limit from finite basis set calculations ” [ Jensen F ( 2005 ) Theor Chem Acc 113 : 267 ]. p. 330–333, 2006.
KÖKSOY, O. Multiresponse robust design: Mean square error (MSE) criterion. Applied Mathematics and Computation, v. 175, n. 2, p. 1716–1729, 2006.
KURTH, S.; MARQUES, M. A. L.; GROSS, E. K. U. Density-Functional Theory.
Encyclopedia of Condensed Matter Physics, p. 395–402, 2005.
LEE, E. P. F. et al. The heat of formation of 2-H heptafluoropropane by ab initio calculations. Chemical Physics Letters, v. 402, n. 1–3, p. 32–36, 2005.
LI, S. et al. Computational calculation of heat of formation for a series of substituted furan derivatives by DFT methods. Journal of Molecular Structure: THEOCHEM, v. 948, n. 1–3, p. 108–110, 2010a.
LI, X. et al. The heats of formation in a series of nitroester energetic compounds: A theoretical study. Journal of Hazardous Materials, v. 165, n. 1–3, p. 372–378, 2009.
LI, Y. et al. Heats of formation of cyano derivatives from ab initio and DFT calculations. Journal of Molecular Structure: THEOCHEM, v. 955, n. 1–3, p. 42–46, 2010b.
MESHHAL, M. M.; EL-DEMERDASH, S. H.; EL-NAHAS, A. M. A thermochemical computational study on hydroxyquinolines and their azulene analogues. Journal of Molecular Structure, v. 1183, p. 70–77, 2019.
NAKAJIMA, Y.; SEINO, J.; NAKAI, H. Relativistic effect on enthalpy of formation for transition-metal complexes. Chemical Physics Letters, v. 673, p. 24–29, 2017.
NELDER, J. A.; MEAD, R. A Simplex Method for Function Minimization. The Computer Journal, v. 7, n. 4, p. 308–313, 1 jan. 1965.
OCHTERSKI, J. W. Thermochemistry in Gaussian. n. Gaussian, Inc, p. 1–19, 2000.
PARK, S. Y.; HUH, S. B.; LEE, J. S. Basis set convergence of correlated calculations on HF , H 2 O , N 2 , CO , and Ne. v. 586, p. 81–90, 2002.
PEREIRA, D. H. et al. Implementation of pseudopotential in the G3 theory for molecules containing first-, second-, and non-transition third-row atoms. The Journal of Chemical Physics, v. 135, n. 3, p. 034106, 21 jul. 2011.
PRASCHER, B. P.; LUCENTE-SCHULTZ, R. M.; WILSON, A. K. A CCSD(T) and ccCA study of mixed silicon hydrides and halides: Structures and thermochemistry. Chemical Physics, v. 359, n. 1–3, p. 1–13, 2009.
ROSSUM, G. VAN. Python Software Foundation. Disponível em: <https://www.python.org/>. Acesso em: 1 set. 2022.
SHAFAGH, I.; HUGHES, K. J.; POURKASHANIAN, M. Modified enthalpies of formation for hydrocarbons from DFT and ab initio thermal energies. Computational and Theoretical Chemistry, v. 964, n. 1–3, p. 100–107, 2011.
VARANDAS, A. J. C. Accurate global ab initio potentials at low-cost by correlation scaling and extrapolation to the one-electron basis set limit. v. 443, p. 398–407, 2007.
















