A Teoria da amostragem (TOS) e Incerteza de medição (MU) para estimativa da incerteza total aplicada em monitoramento de variáveis ambientais em séries temporais.

Home
Trabalhos

A teoria da amostragem (TOS) foi introduzida na química analítica, quimiometria e tecnologias de processos baseada nas referências clássicas da TOS como Pierre Gy e G. Matheron. Em 1950, Pierre Gy iniciou o desenvolvimento do que hoje é conhecido como TOS. Qualquer processo de amostragem por si só gera erros de amostragem. A única forma de eliminar ou minimizar os erros a um nível aceitável é compreender como se originam esses erros de amostragem e são propagados. A TOS combina a parte técnica da amostragem (extrair corretamente a amostra) e a parte estatística para caracterizar a heterogeneidade do alvo da amostragem, para estimar a incerteza gerada pelas operações de amostragem e para generalizar os resultados (PETERSEN; MINKKINEN; ESBENSEN, 2005). Pierre Gy rotulou o erro total de um resultado analítico como o "Erro de Estimativa Global" (GEE). Este erro é composto por duas contribuições fundamentais: O Erro Analítico Total (TAE), que todos os químicos e outros analistas estão bastante familiarizados e o Total Erro de Amostragem (TSE) (F.F. PITARD, 1993; GY, 1998; PATRICIA L. SMITH, 2001). A frequência de amostragem limita o nosso conhecimento de como o processo varia ou flutua rapidamente. Portanto, estabelecer uma frequência de amostragem ideal pode não ser uma tarefa fácil, mas a variografia fornece uma resposta muito informativa através da quantificação da autocorrelação em função da distância entre os pontos ou tempos de amostragem, ou melhor, uma defasagem no tempo ou no espaço (PETERSEN; ESBENSEN, 2005). A variografia foi sugerida como mais um meio empírico de estimar a incerteza de medição a partir das fontes combinadas de amostragem e análise, sendo demonstrado pelo variograma (DE ZORZI et al., 2008). A TOS é uma metodologia completa que avalia o erro total da amostragem associado tanto à amostragem estática (amostragem de dimensão zero ou 0-D) como à amostragem de processo dinâmico (amostragem 1-D). O GEE é determinado pelo variograma como V(0) por meio de extrapolação e é representado por Stotal. A incerteza de medição (MU) descrita no GUM e EURACHEM/CITAC não contempla a amostragem, apenas a medição analítica. Buscando melhorar a estimativa da incerteza total, Esbensen e Wagner (2014) propuseram integrar as duas teorias, já que eram utilizadas isoladamente. Baseando-se na teoria da TOS e UM, o presente trabalhou teve como objetivo avaliar a aplicação destas teorias na estimativa da incerteza de medição de oxigênio dissolvido e temperatura em um corpo hídrico por meio de monitoramento destas variáveis em função do tempo.

A figura 1 mostra a dispersão a autocorrelação (ACF) dos resultados de temperatura e OD em função do tempo para a amostragem in situ. A partir da análise gráfica das séries temporais, observou-se tendências dos parâmetros físico-químicos. Os gráficos c) e d) nos mostram as variáveis temperatura e OD apresentaram um comportamento estacionário. As linhas tracejadas em azul, representa o limite com 95% de confiança, indicando que valores dentro destes limites são estacionários e fora deles são dinâmicos. Como os dados de temperatura e oxigênio dissolvido tiveram a maioria das defasagens em função do tempo dentro destes limites de confiança, considerou-se que os dados foram estacionários. A partir dos variogramas (figura 2) de cada parâmetro físico-químico, obteve-se o valor de V(0) ou do efeito pepita diretamente da equação da regressão linear. V(0) é o intercepto da equação linear. As estimativas das incertezas obtidas por simulação Monte Carlos por meio da calculadora NIST foi de 0,0354 °C para a temperatura e 0,0551 mg L-1 para o OD. Vale ressaltar que a calculadora NIST calcula o valor da incerteza padrão combinada. Observou-se que a calibração do sensor de OD influenciou em 82% sobre as demais componente de incerteza do modelo de medição, enquanto que a calibração do sensor de temperatura foi de 98%. Percebeu-se que a calibração da sonda influenciou significativamente na estimativa da incerteza, o que demonstra a importância de se estimar as incertezas dos resultados para garantir resultados confiáveis. A partir dos resultados, conclui-se que a sonda deve ser calibrada novamente e caso a incerteza persista, deve-se suspender o uso do instrumento para futuras medições. A incerteza da medição analítica foi de 0,011 °C para a temperatura e 0,023 mg·L-1 para o OD, enquanto que a incerteza total da temperatura foi de 0,024 °C e para o OD foi de 0,061 mg·L-1. A incerteza da amostragem foi obtida a partir da incerteza total e analítica, foi de 0,021 °C para a temperatura e 0,056 mg·L-1 para o OD. Portanto, evidenciou-se que a amostragem é a maior fonte de incerteza em uma medição analítica, o que na maioria das vezes é ignorada pelos analistas químicos. O resultado de medição da temperatura foi expresso como (30,8 ± 0,03) °C e OD (5,77 ± 0,06) mg·L-1, onde o número após o símbolo ± é o valor numérico de U=k·uc (uma incerteza expandida) com U determinado por uc e k=2 baseada na distribuição normal para infinitos graus de liberdade, onde U define um intervalo de estimado para se ter uma probabilidade de abrangência de 95%.

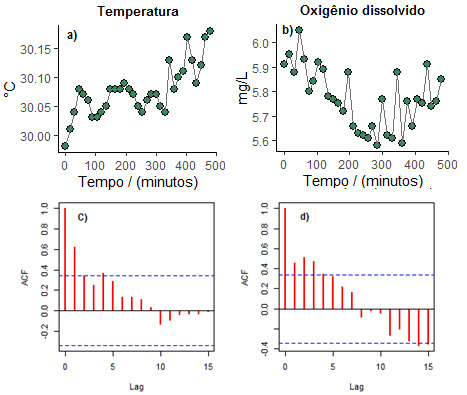
Figura 1: Dispersão a autocorrelação dos resultados

Os gráficos a) e b)mostram as dispersões dos dados de temperatura e oxigênio dissolvido na série temporal, c) e d)os gráficos de autocorrelação.

Figura 2: Variogramas dos parâmetros físico-químicos

Variogramas das séries temporais das variáveis físico-químicas e parâmetros utilizados na estimativa da incerteza da amostragem.

A Teoria da amostragem (TOS) e Incerteza de medição (MU) para estimativa da incerteza total aplicada em monitoramento de variáveis ambientais em séries temporais.

ÁREA

Autores

RESUMO

Palavras Chaves

Introdução

Material e métodos

Resultado e discussão

Conclusões

Agradecimentos

Referências