Estimativa da incerteza de medição por simulação Monte Carlo usando Web calculadora NIST.

ÁREA

Química Analítica

Autores

Corrêa, I. (UFPA) ; Brandão, I. (UFPA) ; Saraiva, A. (ENVIRON) ; Saraiva, D. (UFPA) ; de Matos, A. (FAMAP) ; de Lima, M. (ENVIRON) ; Quintanilha, T. (SAAE) ; Silva, M. (ENVIRON) ; Filho, I. (UFPA) ; da Silva, D. (UFPA)

RESUMO

Dentre várias formas para estimar a incerteza de medição de um método, como por exemplo a de Lei de Propagação da Incerteza (LPU), este trabalho objetiva demonstrar um método de fácil acessibilidade como a calculadora NIST que é baseado na metodologia de Monte Carlo. As técnicas foram aplicadas para calcular a incerteza de medição do potencial hidrogeniônico (pH) em amostras de água, a partir dos resultados encontrados verificamos a equivalência dos resultados, confirmando assim, a validação pelo do método da Lei de Propagação da Incerteza (LPU), a alternativa, ou substituição pela utilização da calculadora NIST como ferramenta de estimativa de incerteza de medição para pH, substituindo o método GUM em medidas diretas.

Palavras Chaves

NIST; Incerteza de medição; Monte Carlo

Introdução

A calculadora de incerteza do Instituto Nacional de Normas e Tecnologia (NIST) é uma aplicação de software para estimar a incerteza de medição associada a uma grandeza de saída definida por um modelo de medição na forma y=f (x1, ..., xn). A função f deve ser especificada como uma fórmula ou algoritmo que, dados os valores dos vetores de entradas, produz um valor do vetor de saída, ou seja, f deve ser vetorizado. As grandezas de entrada sã modeladas como variáveis aleatórias cujas distribuição de probabilidades também tem de ser especificada. A calculadora do NIST foi descrita por Lafarge e Possolo (2015) como uma importante inovação implementada na versão inicial do software que calcula a incerteza baseada nos resultados do método de Monte Carlo. A Calculadora de incerteza de medição do NIST funciona no servidor Web NIST, acessível através de um navegador via Web em https:// uncertainty.nist.gov/. A calculadora NIST está escrito em linguagem R para computação estatística e gráficos (R Core Team, 2015). Informações suscintas e introduções aos conceitos e técnicas básicas para a avaliação da incerteza de medição são detalhadas por Bell (1999) e Hall e White (2018). Outras introduções mais extensivas que incluem exemplos ilustrativos extraídos da pratica da ciência de medição são fornecidas por Possolo e Iyer (2017). A Calculadora de incerteza do NIST avalia a incerteza de medição através da aplicação de dois métodos diferentes: O método introduzido por Gauss (1823) e difundido por Kline e McClintock (1953), em particular nas comunidades de física e engenharia, sendo este método descrito sucintamente por Taylor e Kuyatt (1994) e detalhado no Guia de Avaliação de incerteza de medição-GUM (JCGM, 2008a ) e o método Monte Carlo descrito por Morgan e Henrion (1992) no contexto

Material e métodos

As indicações de pH nas amostras de água foram realizadas com sonda multiparâmetro YSI 556 MPS com calibração rastreável ao INMETRO. A amostra composta foi constituída de 33 alíquotas de amostras simples coletada em intervalos de 15 minutos, entre 9h e 17h, em novembro de 2019, no Rio Guamá, na cidade de Belém-PA. Para a estimativa da incerteza de medição analítica foram consideradas as seguintes fontes de incertezas: Incerteza da repetibilidade da medição, resolução do instrumento, variação de temperatura em relação à temperatura de calibração, ajuste com soluções padrões, calibração da sonda e precisão. A partir do certificado de calibração, foram obtidas informações do erro sistemático (tendência) para corrigir os resultados, bem com o valor da incerteza expandida, fator de abrangência (k) e o tipo de função de densidade de probabilidade (pdf). A estimativa da incerteza de medição foi realizada pelo método GUM que tem uma abordagem frequencista, bem como pelo método de Monte Carlo por inferência bayesiana, no qual foi desenvolvida a calculadora NIST. Os resultados foram comparados em função da complexidade dos cálculos, agilidade e aplicação, além de transmitir mais confiabilidade aos resultados de pesquisas das universidades.

Resultado e discussão

A estimativa da incerteza de medição obtida pelo método GUM, foi calculada usando a tabela abaixo 1 e as informações obtidas pelo método de Monte Carlo estão na figura 1. Estimativa da densidade de probabilidade da quantidade produzida (linha azul sólida), e densidade de probabilidade (linha vermelha pontilhada) de uma distribuição gaussiana com a mesma média e desvio padrão que a quantidade produzida. Neste caso, a aproximação gaussiana é muito precisa. Os resultados da estimativa da incerteza de medição para a variável pH obtidos pelo método GUM e Monte Carlo corroboram-se, evidenciando que a calculadora NIST pode ser empregada para estimar a incerteza de uma infinidade de variáveis físicas e químicas. Ressaltamos que o uso da calculadora NIST exige apenas informações da quantidade variáveis de entrada, o tipo de pdf, graus de liberdade, cálculos simples de média, desvio-padrão e desvio-padrão da média, além da definição de modelo de medição da grandeza de saída, bem diferente da exigência de cálculo de derivadas parciais, coeficientes de contribuição de Kessel, equação de Welch-Satterthwaite exigidos pelo GUM, o que torna a estimativa muito trabalhosa. A partir da análise do coeficiente de contribuição proposto por Kessel et al (2006) obtidos pelos dois métodos, foi possível constatar que a componente que a calibração do pHmetro, bem como a precisão intermediária foram as maiores contribuições na avaliação da incerteza de medição.

Cálculo de incerteza pelo método GUM


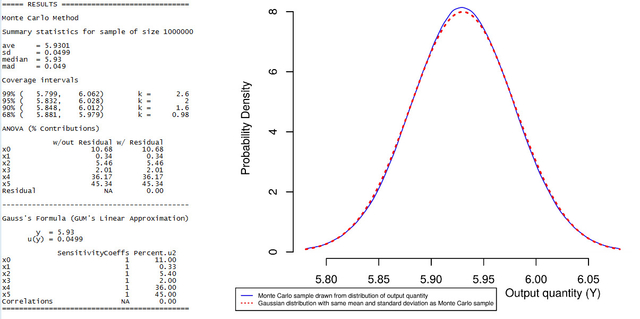
Estimativa da densidade de probabilidade.

Conclusões

A estimativa de incerteza de medição para medidas diretas usando a calculadora NIST foi bastante eficiente quando comparada com o método GUM, os resultados obtidos pelos dois métodos concordam, no entanto, a calculadora NIST fornece a estimativa com mais agilidade, sem muito esforço para a elaboração de planilhas eletrônicas e pode ser aplicada em diversas pesquisas acadêmicas. Portanto, a calculadora NIST pode substituir o método GUM para medidas diretas.

Agradecimentos

Referências

T. Lafarge and A. Possolo. The NIST Uncertainty Machine. NCSLI Measure Journal of Measurement Science, 10(3):20–27, September 2015.
R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2015.
S. Bell. A Beginner’s Guide to Uncertainty of Measurement. Number 11 (Issue 2) in Measurement Good Practice Guide. National Physical Laboratory, Teddington, Middlesex, United Kingdom, 1999. URL www.npl.co.uk/publications/ guides/a-beginners-guide-to-uncertainty-of-measurement. Amendments March 2001.
B. D. Hall and D. R. White. An Introduction to Measurement Uncertainty. Measurement Standards Laboratory of New Zealand, Lower Hutt, New Zealand, 2018.
A. Possolo and H. K. Iyer. Concepts and tools for the evaluation of measurement uncertainty. Review of Scientific Instruments, 88(1):011301, 2017. doi: 10.1063/1. 4974274.
C. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. In Werke, Band IV, Wahrscheinlichkeitsrechnung und Geometrie. Könighlichen Gesellschaft der Wissenschaften, Göttingen, 1823. gdz.sub.uni-goettingen.de/
S. J. Kline and F. A. McClintock. Describing uncertainties in single-sample experiments. Mechanical Engineering, 75(1):3–8, 1953.
M. H. DeGroot and M. J. Schervish. Probability and Statistics. Addison-Wesley, 4th edition, 2011.
Joint Committee for Guides in Metrology. Evaluation of measurement data — Guide to the expression of uncertainty in measurement. International Bureau of Weights and Measures (BIPM), Sèvres, France, 2008a. URL www.bipm.org/en/publications/ guides/gum.html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 100:2008, GUM 1995 with minor corrections.
Joint Committee for Guides in Metrology. Evaluation of measurement data — Supplement 2 to the “Guide to the expression of uncertainty in measurement” — Extension to any number of output quantities. International Bureau of Weights and Measures (BIPM), Sèvres, France, 2011. URL www.bipm.org/en/publications/guides/gum. html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 102:2011.
F. E. Satterthwaite. An approximate distribution of estimates of variance components. Biometrics Bulletin, 2(6):110–114, December 1946.
B. N. Taylor and C. E. Kuyatt. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results. NIST Technical Note 1297. National Institute of Standards and Technology, Gaithersburg, MD, 1994.
B. L. Welch. The generalization of ‘Student’s’ problem when several different population variances are involved. Biometrika, 34:28–35, January 1947.
INMETRO, I. N. DE M., Qualidade e Tecnologia. DOQ-CGCRE-019 - Exemplos de Estimativa de Incerteza de medição em Ensaios Químicos, 2013.
INMETRO, I. N. DE M., Qualidade e Tecnologia. Vocabulário Internacional de Metrologia: Conceitos Fundamentais e Gerais e Termos Associados (VIM 2012). 1a Edição Luso-Brasileira ed. Duque de caxias - RJ: [s.n.].
KESSEL, R.; KACKER, R. & BERGLUND, M. Coefficient of contribution to the combined standard uncertainty, Metrologia Vol. 43, p.189-195, 2006.