Aplicação de inteligência artificial para desenvolvimento de um filtro de redução de ruído em dados de curvas cinéticas.

ISBN 978-85-85905-25-5

Área

Química Tecnológica

Autores

Arraes, M.L. (ESTÁCIO RECIFE) ; Silva, J.P. (ESTÁCIO RECIFE) ; Cavalcanti, D.E.S. (UNINABUCO) ; Aquino, R.V.S. (UFPE) ; Barbosa, A.A. (UFPE) ; Souza, T.P.C. (UFRPE) ; Rossiter Sa da Rocha, O. (UFPE) ; Marcos Francisco da Silva, J. (UFPE)

Resumo

Este trabalho propõe o uso de um filtro não linear utilizando redes neurais artificiais multicamadas para redução de ruídos em curvas cinéticas. Diversos tipos de redes foram estudadas, dados sintéticos foram gerados para treinamento das redes, o coeficiente de determinação ajustado (R²) foi utilizado como parâmetro de desempenho, o melhor resultado para dados unidimensionais foi uma rede do tipo 9:1, com nove entradas (valores com ruído) e uma saída (valor central sem ruído), que resultou em um R² ajustado final de 0.978 para o conjunto de casos treinados. Aplicando a processos oxidativos avançados foi possível reduzir o ruído da cinética de degradação do azul brilhante FCF, utilizando H₂O₂/UV, desta forma foi possível tornar o R² ajustado da cinética de 0.9969 para 0.9989.

Palavras chaves

redes neurais; filtro; cinética química

Introdução

Durante a obtenção de resultados experimentais é comum a ocorrência de flutuações nos valores obtidos, esse fato se deve a pequenas perturbações aleatórias provenientes de diversas fontes, tais como, oscilações elétricas, flutuações na temperatura, e até mesmo erro do operador, o ruído gerado destas perturbações pode esconder a real tendência de dados e curvas (WALCZAK, p.4, 2000; BROWN, p. 24-25, 1986), para isso diversos trabalhos se propõem ao desenvolvimento de filtros de remoção de ruído (CHEN et al, 2007; BARONE et al, 2007; KUO e MORGAN, 1999) porém os filtros não lineares acabam recaindo em processos complexos ou computacionalmente desfavoráveis, em contrapartida os filtros lineares são simples, mas muitas vezes não atingem o nível adequado de remoção de ruído (PRIVMAN, p. 118-119, 2011; BROWN, p. 1-2, 1986). A Inteligência Artificial (IA) permite que diversas tarefas típicas do comportamento humano possam ser executadas por dispositivos eletrônicos, isto é, que sejam treinadas para cumprir tarefas específicas a partir do processamento de grandes volumes de dados e reconhecimento de um padrão nesses dados, os conceitos iniciais de IA foram desenvolvidos por McCulloch e Pitts (1943). Com a ampliação do uso da inteligência artificial e redes neurais, e cada vez mais têm sido aplicados nos processos laboratoriais e industriais, aproveitando a difusão do conhecimento é possível aplicar estes métodos também na redução do ruído dos dados obtidos por sensores e equipamentos em um processo qualquer, o tipo de filtro definido por uma rede neural artificial (RNA) é chamado de filtro neural, e inicialmente foi idealizado por Arakawa and Harashima (1990). No filtro neural pontos vizinhos aos que se deseja remover o ruído são utilizados como entrada de uma rede neural. Os processos oxidativos avançados também estão sujeitos a ocorrência de ruídos de diversos tipos durante a cinética de degradação (BARBOSA et al, 2019; NASCIMENTO et al, 2017; AQUINO et al, 2019; ROCHA et al, 2017) a existência de ruídos no resultado experimental pode comprometer os resultados cinéticos obtidos ou até mesmo diminuir a quantidade de informação útil disponível (BROWN, p. 25, 1986). Desta forma fica clara a necessidade da aplicação de filtros em dados para redução de ruído. O presente trabalho visou desenvolver um método de redução de ruídos em curvas cinéticas, especificamente em processos oxidativos avançados, testando diversos tipos de redes neurais, para isso dados sintéticos foram gerados no Scilab simulando comportamentos comuns em situações práticas de reações químicas, mais de 2400 casos foram utilizados para treinar as diversas redes neurais, de diversas estruturas diferentes, o programa utilizado para treinamento foi o Neural Educator, software desenvolvido exclusivamente para a pesquisa em questão.

Material e métodos

A metodologia consistiu em testar tipos diferentes de redes neurais para verificar qual se adéqua melhor à remoção de ruído em curvas cinéticas, para isso sinais foram gerados artificialmente utilizando o Scilab. As curvas geradas foram adicionadas de ruído, o qual foi definido como tendo amplitude variável. foram utilizados ao todo 2400 casos de treinamento.Os casos de treinamento forma organizados em conjuntos de 9 entradas e 1 saída. 3 arquivos de dados de treinamento foram gerados, onde a rede neural em treinamento fazia o treinamento por lotes de dados. As RNAs são compostas por entradas, camadas ocultas e saídas com diferentes estruturas e diferentes números de neurônios. Diversas estruturas de redes neurais foram testadas (9:1), (9:4:1), (9:8:1) e (9:12:1), o número inicial representa a quantidade de entradas (dados com ruído) o último número representa a saída (um ponto sem ruído) e o número central, quando há, representa o número de neurônios em uma camada oculta intermediária. O software utilizado para o ajuste neural foi desenvolvido pelo grupo de pesquisa utilizando o Unity 3D©, o software desenvolvido foi capaz de ajustar as diversas RNAs aos dados durante a fase de aprendizagem, o método de aprendizagem foi baseado na otimização de enxame de partículas, busca aleatória e algoritmo genético, em parte apresentado por Kennedy e Eberhart (1995). O critério de erro adotado foi o erro absoluto médio e o coeficiente de determinação ajustado (R²). Foi utilizada uma rede neural alimentada adiante, a função de ativação adotada foi sigmóide entre 1 e -1. Para realizar a análise da RNA, os valores de entrada foram normalizados e estabelecidos entre -1 e 1 [-39.39347, 97.16517] da mesma forma para a saída [-1,1]→[-33.17026, 97.3], a fim de garantir que o treinamento não faça a rede fugir para uma zona de saturação, conforme exposto por Haikin (1999). O tempo de treinamento utilizado foi de 1800 segundos para atingir um erro residual limite. Todos os treinamentos foram realizados em um PC comum. A rede ótima obtida do estudo foi aplicada a um caso de degradação para verificar a eficácia do método. O processo de degradação foi realizado em um reator fotocatalítico de bancada contendo lâmpada germicida UVC (Ilumisampa, 20W), agitadores magnéticos e recipientes cilíndricos de vidro com dimensões de 9x5,5 cm. Seguindo outros trabalhos da literatura (BARBOSA et al, 2019; NASCIMENTO et al, 2017; AQUINO et al, 2019; ROCHA et al, 2017). O teste foi realizado com uma solução do corante alimentício azul brilhante FCF (fórmula molecular C₃₇H₃₄N₂Na₂O₉S₃, índice de cor 42090, obtido de F. Trajano aromas e ingredientes LTDA). A dose de peróxido de hidrogênio (50% v/v, Coremal Pochteca LTDA) utilizada foi baseada a partir de cálculos estequiométricos. Para avaliar a descoloração, a partir de medidas de absorbância, foi utilizado um espectrofotômetro UV-Vis (Spectroquant Pharo 300) a partir do da absorção no comprimento de onda máximo do corante (λ = 630 nm).

Resultado e discussão

Os dados gerados para treinamento foram definidos por funções representativas de sistemas químicos, a partir das diversas curvas criadas utilizando um script em Scilab foi possível adicionar ruído, para que houvesse um comparativo dos mesmos dados com e sem ruído, o ruído adicionado tinha amplitude variável a cada curva gerada, com o intuito de cobrir uma ampla gama de possibilidades. Os dados gerados foram divididos em 3 arquivos organizados de forma a serem reconhecidos pelo software desenvolvido. Associando 9 pontos com ruído a uma saída sem ruído. Diversos tipos de redes foram testadas para se verificar qual tinha o melhor desempenho, foram elas (9:1), (9:4:1), (9:8:1) e (9:12:1) como exposto pela metodologia. Os resultados obtidos estão expostos na Tabela 1. Tabela 1 – Resultados obtidos dos treinamentos das redes neurais Rede Arquivo de dados Numero de parâmetros livres Erro absoluto médio R² R² ajustado Tempo de treinamento (s) 9 1 F 1 11 1,652648 0,9920533 0,9917064 1800,025 F 2 11 2,980382 0,9597521 0,9576236 1800,039 F 3 11 1,614204 0.9796286 0,9782622 1800,029 9 4 1 F 1 46 1,599811 0,991517 0,9897188 1800,028 F 2 46 2,736030 0,9709115 0,963177 1800,016 F 3 46 2,061707 0,9676653 0,956135 1800,039 9 8 1 F 1 90 7,113652 0,9897679 0,9844449 1800,005 F 2 90 2,387422 0,9808192 0,9674372 1800,001 F 3 90 1,631204 0,9800913 0,9590116 1800,005 9 12 1 F 1 134 1,478016 0,9919661 0,9836208 1800,158 F 2 134 1,942187 0,9881155 0,9693801 1800,029 F 3 134 1,889585 0,9675796 0,8616202 1800,079 Na tabela 1 é possível observar detalhes sobre os treinamentos de cada rede, as respectivas estruturas estão expostas na primeira coluna, a segunda coluna é referente aos arquivos utilizados no treinamento, cada um contendo 800 casos de treinamento, na terceira coluna há o número de parâmetros de cada rede, incluindo pesos e bias, essa informação permite verificar se há superajustamento dos dados, como o número de parâmetros é muito inferior ao número de casos de treinamento não há risco de superajuste. A quarta coluna é referente ao erro absoluto médio de cada rede após treinar sobre o conjunto de dados, sendo que cada rede treinou sequencialmente em cada arquivo de dados, por tanto o terceiro resultado já passou pelo treinamento de todos os dados, observando apenas o erro absoluto médio como critério para definir o melhor resultado seria possível concluir que o melhor resultado seria na rede 9 4 1, porém esse critério não é o único a ser levado em consideração. A quinta coluna da tabela 1 é referente ao coeficiente de determinação, R², que é referente a qualidade do ajuste entre os dados e a rede, estando no intervalo [0,1], valores próximos de 1 representam um bom ajuste, novamente a rede 9 4 1 encontrou o melhor resultado. A sexta coluna é referente ao coeficiente de determinação ajustado, que penaliza o R² a cada parâmetro incluído no modelo, desta forma o melhor resultado foi obtido pela rede 9 1 com R² ajustado 0,9782 após o treinamento com os 3 conjuntos de dados, levando em consideração simplicidade e precisão este foi o melhor resultado. A sétima coluna é referente ao tempo de treinamento, fixado em 1800 segundos. Partindo do melhor resultado da tabela 1, a rede 9 1 é detalhada na Figura 1. Figura 1 – Estrutura ótima obtida durante os treinamentos das redes neurais. Na Figura 1 é possível observar que a rede recebe valores normalizados no intervalo [-39,39347, 97,16517] -> [-1,1] e dessa forma o valor central dos 9 valores de entrada tem o ruído removido, com saída também normalizada [-1,1] -> [-33,17026,97,3], ainda na Figura 3 é possível observar os valores de pesos e bias resultantes do treinamento.A rede resultante pode ser implementada em qualquer programa a partir do pseudo-código a seguir. %Normalização da entrada para i=1:9 Entrada(i) = 2*(Entrada(i)+39,39347)/136,5586 - 1 fimpara %Cálculo da rede Saída=1,451795*(2/(1+exp(-1*(0,02124606*Entrada(1)-0,02318731*Entrada(2)-0,01913163*Entrada(3)+0,380681*Entrada(4)+1,003919*Entrada(5)+0,3451191*Entrada(6)-0,110536*Entrada(7)+0,02409568*Entrada(8)-0,0824337*Entrada(9)-0,053719)))-1) %Denormalização da saída Saida = 65,23513* Saída +32,06487 O pseudo-código acima pode ser subdividido em 3 partes: normalização da entrada, cálculo da rede e denormalização da saída. E pode ser aplicada em outros trabalhos. A degradação do azul brilhante FCF (C₃₇H₃₄N₂Na₂O₉S₃) foi executada seguindo a metodologia descrita, e resultou na curva de degradação da substância utilizando UV/H₂O₂. Um ajuste cinético de pseudo-primeira ordem foi executado para servir como referência cinética de degradação, com valor de K=0.0506 min-1. Gerando a Equação 1. 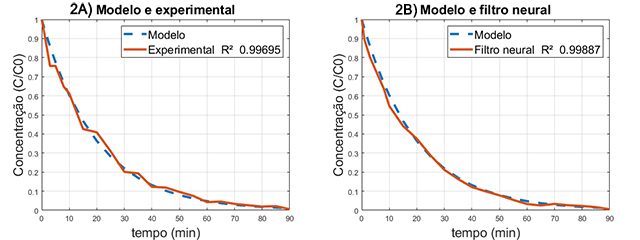C(t)=exp(-0,0506*t) (1) As curvas resultantes e os dados experimentais e do modelo cinético estão expostos na Figura 2A. Figura 2 – A) Comparação dos dados experimentais e do modelo cinético B) Comparação dos dados experimentais filtrados pelo filtro neural e do modelo cinético.. Na Figura 2A é possível observar a concordância entre os resultados experimentais e os dados gerados pelo modelo, o coeficiente de determinação gerado foi de 0,99695, demonstrando um ajuste adequado, ainda na Figura 2 é possível observar pequenas flutuações dos dados experimentais ao longo da curva, mostrando que houve ruído experimental. O método discutido neste trabalho pode ser utilizado para remover essas variações aleatórias, diminuindo a amplitude do ruído. Na Figura 2B é possível observar os dados experimentais depois de filtrados pelo método exposto neste trabalho, os 4 pontos iniciais e os 4 pontos finais foram filtrados seguindo uma média simples entre os pontos vizinhos, pois não seria possível aplicar a rede neural resultante, pois são necessários 9 pontos para se aplicar o filtro neural. Fica verificado a partir da Figura 2A que a amplitude do ruído é reduzida ao ponto que a concordância entre o modelo e os dados torna o R² igual a 0,99887, valor superior ao encontrado sem o uso do filtro neural. Desta forma fica comprovado que o uso do filtro neural pode melhorar a concordância entre os dados e o modelo, diminuindo a importância dos erros experimentais que venham a ocorrer.

Estrutura ótima obtida durante os treinamentos das redes neurais.


A) Comparação dos dados experimentais e do modelo cinético B) Comparação dos dados experimentais filtrados pelo filtro neural e do modelo cinético

Conclusões

Todo dado experimental obtido está sujeito a flutuações aleatórias de diversas origens, diversos métodos podem ser aplicados para reduzir a influência destes ruídos, o método apresentado neste trabalho utilizou redes neurais para aplicar inteligência artificial na redução destes ruídos, diversas redes neurais foram testadas, sendo a rede mais simples, a rede (9 1) a que teve o melhor desempenho, gerando uma curva filtrada com erro percentual reduzido para 1,1% em média de diferença entre a curva sem ruído (ideal) e a curva com ruído. Levando a um R² ajustado de 0,9782. A rede desenvolvida foi aplicada em um processo cinético de degradação do azul brilhante FCF, e permitiu a redução de ruídos experimentais nos pontos resultantes, melhorando o ajuste entre o modelo e os dados de 0,99695 para 0,99887 segundo o coeficiente de ajustamento. Este aumento pode ser mais significativo caso os dados tenham uma amplitude maior de ruído. O trabalho conclui que o filtro neural é um método eficiente na redução de ruídos cinéticos, permitindo maior flexibilidade na obtenção de dados, que podem ser filtrados durante o tratamento de dados. O uso de inteligência artificial apresenta cada vez mais potencial de aplicação em diversas áreas do conhecimento, incluído nos processos químicos.

Agradecimentos

Os autores agradecem ao apoio do Laboratório de Engenharia de Alimentos da Universidade Federal de Pernambuco e do programa de pesquisa produtividade do Centro Universitário Estácio Recife para a realização do trabalho.

Referências

AQUINO, R. V. S.; BARBOSA, A. A.; RIBEIRO, L. B.; OLIVEIRA, A. F. B.; SILVA, J. P. ; AZOUBEL, P. M.; ROCHA, O. R. S. Degradation of leaf green food dye by heterogeneous photocatalysis with TiO over a polyethylene terephthalate plate. CHEMICAL PAPERS (ONLINE), v. 1, p. 1-12, 2019.

ARAKAWA, K.; HARASHIMA, H. A nonlinear digital filter using multilayerd neural networks. Proc. IEEE Int. Conf. Communications ’90, v. 2, p. 424-428, 2013.

BARBOSA, A. A.; AQUINO, R. V. S.; OLIVEIRA, A. F. B.; DANTAS, R. F.; SILVA, J. P.; DUARTE, M. M. M. B.; ROCHA, O. R. S. Development of a new photocatalytic reactor built from recyclable material for the treatment of textile industry effluents. Desalination and Water Treatment, v. 151, p. 82-92, 2019.

BARONI, C.; GALDI, A.; PAGANO, S. Quaranta Experimental technique for reducing contact and background noise in voltage spectral density measurements. Review of Scientific Instruments, v. 78-9, 2007.

BROWN, S.D. THE KALMAN FILTER IN ANALYTICAL CHEMISTRY. Anal. Chim. Acta, v. 181, 1986.

CHEN, Y.; DAS, M. An automated technique for image noise identification using a simple pattern classification approach. Proceedings of MWSCAS 07, IEEE Computer Society, p. 819-822. 2007.

HAYKIN S. Redes neurais, princípios e prática. Editora Artmed AS. 2ª edição. 2004.

NASCIMENTO JUNIOR, W. J.; ROCHA, O. R. S.; DANTAS, R. F.; BARBOSA, A. A.; SILVA, J. P. Kinetic study of food dyes removal from aqueous solutions by solar heterogeneous photocatalysis with artificial neural networks and phytotoxicity assessment. Desalination and Water Treatment, v. 104, p. 304-314, 2017.

KENNEDY, J.; EBERHART, R. Particle swarm optimization. IEEE International Conference, 1995.

MCCULLOCH W.; PITTS W. A Logical Calculus of Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biophysics, v. 5, p. 115–133, 1943.

PRIVMAN, V. Control of Noise in Chemical and Biochemical Information Processing. Special Issue: Molecular and Biomolecular Information Processing Systems. v. 51, i. 1. p. 118-131. 2011.

ROCHA, O. R. S.; DANTAS, R. F.; JUNIOR, W. J. N.; FUJIWARA, Y.; DUARTE, M. M. M. B.; SILVA, J. P. Kinetic study and modelling of cephalexin removal from aqueous solution by advanced oxidation processes through artificial neural networks. Desalination and Water Treatment, v. 92, p. 72-79, 2017.

KUO, S. M.; MORGAN, D. R. Active Noise Control: A Tutorial Review. PROCEEDINGS OF THE IEEE, v. 87, nº 6, 1999.

WALCZAK, B. Wavelets in chemistry. Data handling in science and technology. v. 22. 2000.