ESTIMATIVA DAS PERDAS DE CARGAS PELA EQUAÇÃO DE BERNOULLI EM TUBULAÇÕES DISTINTAS

ISBN 978-85-85905-25-5

Área

Química Tecnológica

Autores

Cornélio, J.L. (UEG-CCET) ; Mota, D.C.M. (UEG-CCET) ; Silva, D.A. (UEG-CCET) ; Costa, O.S. (UEG-CCET)

Resumo

A equação da continuidade de Bernoulli considerada para fluidos reais, determina de forma teórica a perda de carga (hp) de um sistema, que consiste na perda de energia de um fluido em escoamento. A perda de carga é proporcional a perda de pressão, perceptível experimentalmente, ao considerar sistemas de baixas pressões. Ensaios laboratoriais foram realizados com duas tubulações uma retilínea e outra contendo redução no diâmetro. Vazões médias, altura piezométrica, velocidade e perda de carga contínua foram estimadas. Constatou-se que a hp da tubulação com redução (49,44 cm) foi maior que na tubulação retilínea (49,35 cm), comprovado pela relação da perda de pressão e das vazões medias.

Palavras chaves

Tubulação; Perda de carga; Equação de Bernoulli

Introdução

As tubulações são comumente utilizadas em industrias e na vida cotidiana, ao serem capazes de transportar uma energia de um ponto a outro do sistema. O escoamento em tubos de fluidos reais apresenta uma perda de energia, esta perda é devido ao atrito do fluido entre as paredes do tubo e entre as diversas camadas de escoamento, e é influenciada pela variação do diâmetro do tubo, a viscosidade, velocidade e pressão do fluido (MILIAVACA et al., 2004; VIANNA JUNIOR; CAMPELO JUNIOR, 2013). A perda de carga no escoamento é proporcional a perda de pressão do fluido ao decorre da tubulação, utilizando piezômetro pode-se em baixas pressões determinar a perda de carga. Estudos experimentais são importantes para a determinação destas perdas para estabelecer a vazão necessária, volume do fluido que atravessa por uma certa seção por unidade de tempo, objetivada no uso da tubulação em instalações (BRUNETTI, 2008; ÇENGEL; CIMBALA, 2015). A determinação da perda de carga, pode ser determinada pelo teorema de Daniel Bernoulli, que para um fluido real, defini que há uma diferença entre a energia do primeiro para o segundo ponto de medição do tubo de escoamento, denominada essa diferença de perda de carga (hp), sendo p= pressão; v= velocidade do fluido;z= altura em relação a um referencial e γ= massa específica do fluido, conforme Equação 1 (VIANNA JUNIOR; CAMPELO JUNIOR, 2013). Z_1+p_0/γ+v_1/2g=Z_2+p_0/γ+(v_2^2)/2g+hp Equação 1: Equação da continuidade de Bernoulli. O presente trabalho teve como objetivo principal estimar a perda de carga entre duas tubulações distintas, uma retilínea e outra com redução pela equação de Bernoulli. E especificou-se determinar as alturas piezométricas e pressões ao longo da tubulação e definir a vazão e a velocidade do fluido.

Material e métodos

Os experimentos foram desenvolvidos no Campus de Ciências Exatas e Tecnológicas da Universidade Estadual de Goiás, realizados no sistema hidráulico - composto por um reservatório acoplado à duas tubulação. A perda de carga foi avaliada em um comprimento de 1,15m de tubulação, por três piezômetros, distanciados por aproximadamente 28 cm ao longo da tubulação. O reservatório foi preenchido de água até altura H, o registro no final da canalização foi aberto com apenas um giro e o nível de água foi mantido constante, um escoamento em regime permanente. As tubulações I (com redução) e I (retilínea) foram ensaiadas individualmente, com mesma abertura de registro. As vazões foram determinadas pelo método volumétrico e obteve-se o valor em triplicata. As alturas piezométricas medidas com trena. E as perdas de cargas contínuas foram estimadas pela equação de Bernoulli.

Resultado e discussão

As medidas piezométricas – altura da coluna de fluido nos piezômetros – para as tubulações com redução (I) e retilínea (II) foram estabelecidas nos pontos definidos e apresentou em cada caso um padrão característico, conforme da Figura 1. Figura 1. Alturas piezométrica em função do comprimento em comparação para as tubulações. Para tubulação II constata-se um rebaixamento consecutivo do nível da coluna de água no interior dos piezômetros. E na tubulação I observa-se um acrescentamento grande no nível da coluna de água no interior dos piezômetros do primeiro ponto para o segundo e um caimento do segundo para o terceiro, em razão da redução do tubo entre os pontos P1 e P2 e a continuidade entre os pontos P2 e P3. As vazões para as tubulações I e II foram, respectivamente, 28,65 cm3s−1 e 43,67 cm3s−1, observando então que a vazão na tubulação I é menor por conta da maior pressão exercida nesta, logo o fluido possui maior obstáculo para o escoamento. Outra avaliação realizada, se refere à relação entre perda de pressão e perda de carga distribuída. A pressão varia conforme a variação da medida das alturas piezométricas e assim constata-se uma pressão maior na tubulação I. A perda de carga nas tubulações foi calculada através da equação da continuidade de Bernoulli onde considera-se que o ponto 1 se encontra na superfície, com velocidade igual a zero. Assim a perda de carga contínua (hp) das tubulações, correspondem para tubulação I de 49,44 cm e tubulação II de 49,35 cm, constatando que a perda de carga na tubulação I é maior que na II, em razão da maior pressão exercida na tubulação I, em razão da redução do diâmetro, resultando assim num aumento da velocidade média do escoamento para que se mantivesse constante a vazão.

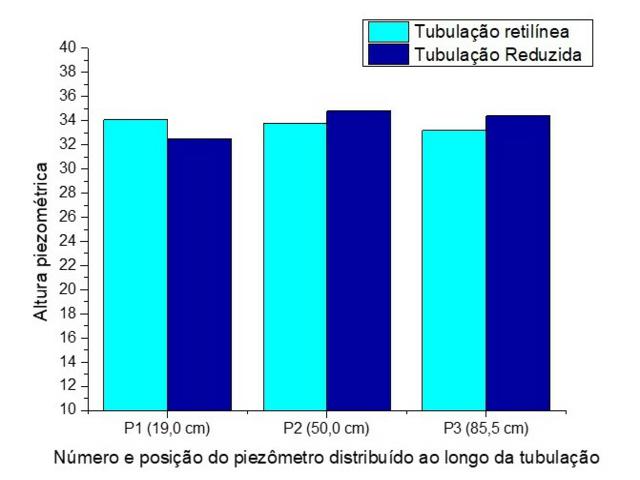
Alturas piezométrica em função do comprimento em comparação para as tubulações.

Conclusões

A perda de carga pode ser relacionada intrinsicamente com as medidas piezométricas, onde se observa ao comparar o escoamento nas duas tubulações, que aquela em que o fluido exerce maior pressão a perda de carga é maior, onde na tubulação reduzida a perda de 49,44 cm e tubulação retilínea de 49,35 cm. Esse fenômeno constitui do aumento da velocidade, devido a redução do diâmetro resultando num maior número de colisões e assim maior perda, desta forma avalia- se alguns aspectos para instalação industrial que visa analisar a perda de carga e pressão nas tubulações em busca de maior eficiência.

Agradecimentos

A CCET-UEG e aos técnicos e estagiários dos laboratórios de Química-CCET/UEG.

Referências

BRUNETTI, F. Mecânica dos fluidos. 2 ed. São Paulo: Pearson Prentice Hall, 2008.

ÇENGEL, Y. A.; CIMBALA, J. M. Mecânica dos fluidos: fundamentos e aplicações. 3 ed. São Paulo: AMGH Editora Ltda., 2015.

MILIAVACA, A.; CUNHA, J. T.; DIETRICH, L. B.; MAGALHÃES, T. S. Medição de perda de carga distribuída em tubulações. Porto Alegre, Universidade Federal do Rio Grande do Sul, Departamento de Engenharia Mecânica, 2004.

VIANNA JUNIOR, W.; CAMPELO JUNIOR, L. R. Velocidades ideias de escoamento de fluido hidráulico em tubulações e dutos de Manifolds. In: Fórum MDA South América. São Paulo, mar. 2013.