ESTUDO DA FORMAÇÃO DA CAMADA DE CONCENTRAÇÃO DE SAIS NA SUPERFÍCIE DE MEMBRANAS

ISBN 978-85-85905-25-5

Área

Química Tecnológica

Autores

Lira, R.H.P. (UFAL) ; Neto, S.R.F. (UFCG)

Resumo

A utilização dos processos de separação por membranas têm se destacado no setor da dessalinização por osmose reversa, usando como força motriz a pressão transmembranica numa membrana semipermeável. O objetivo deste trabalho foi avaliar a formação da camada de concentração na superfície de membranas empregando a fluidodinâmica computacional. As equações de conservação de massa, momento linear e de matéria, bem como as equações de fluxo de difusão foram definidas visando prever a formação da camada de concentração de polarização. Todas as simulações foram realizadas usando o programa comercial Ansys-CFX® 15.0. Os resultados das simulações mostraram uma boa representatividade dos fenômenos de transferência envolvidos no processo de separação em função das variações de velocidade e pressão.

Palavras chaves

Membrana; Modelagem CFD; Concentração-polarização

Introdução

A capacidade de produção de água tem aumentado nas ultimas décadas nos mais diversos setores da indústria através dos processos de separação por membranas (PSM) destacando-se no setor da dessalinização por osmose reversa (RO) para produção de água potável a partir da água salobra e/ou do mar. Nesse cenário a RO destaca-se como alternativa por apresentar grandes fluxos de permeabilização, alta seletividade e menor custo quando comparado com outros processos de dessalinização, como os processos técnicos que utilizam intensa quantidade de energia. Os PSM utilizam a pressão como força motriz para retirada dos solutos dissolvidos e suspensos na água. A membrana é um filme permeável que separa duas fases atuando como uma barreira seletiva entre essas fases e com a capacidade transportar determinados componentes. A permeação ocorre devido à diferença de pressão aplicada entre os canais de alimentação e permeado. O fluxo de água através da membrana é calculado de acordo com o mecanismo de transporte de solução-difusão, BAKER (2004). EL-DESSOUKY e ETTOUNEY (2002) comentam que dessa forma têm-se dois importantes fatores para o bom funcionamento do sistema, um baixo índice de incrustação na membrana e um alto desempenho do módulo, promovido pela redução da concentração de polarização. A concentração de polarização é o termo utilizado para descrever o acúmulo de soluto próximo à superfície da membrana onde a concentração do soluto é maior do que a encontrada na corrente da alimentação durante o processo de separação. De acordo com SCHNEIDER e TSUTIYA (2001), a camada de sais junto à superfície da membrana é formada devido ao transporte convectivo dos sais para a membrana pelo movimento da água e a difusão dos sais para longe da membrana, provocada pelo gradiente de concentração estabelecido na vizinhança da fronteira, devido semipermeabilidade da membrana os sais presentes na solução de alimentação são retidos na interface da membrana. Se a quantidade de sais na camada de concentração de polarização ultrapassar o limite de solubilidade os sais poderão precipitar na superfície membrana, provocando aumento na pressão, diminuição no fluxo de permeado, aumento da passagem de soluto através da membrana e favorecimento de incrustações por deposição. Consequentemente levando a um aumento nos custos de operação e manutenção, diminuição no rendimento do sistema e redução da qualidade do produto final. No processo de RO a permeabilidade pode ser afetada pela concentração e tipo de soluto presente na solução de alimentação, sendo o controle dos processos de precipitação de sais um dos principais condicionantes de projeto. A forma mais eficaz, para evitar a precipitação de sais, é a operação da membrana dentro de limites, que impedem que as concentrações de sais retidos atinjam valores próximos aos limites de solubilidade (SCHNEIDER e TSUTIYA, 2001). A aplicação da fluidodinâmica computacional a processos de separação por membranas tem sido feita por diversos pesquisadores com estudos relacionados à hidrodinâmica e transferência de massa. GHIDOSSI et al (2006) dizem que a fluidodinâmica computacional é uma ferramenta importante para a compreensão e desenvolvimento dos processos com membranas. FLETCHER e WILEY (2004) estudaram os efeitos das forças de campo na separação de sais em um módulo de membrana plana usando as equações semelhantes às utilizadas pelos mesmos autores em trabalho anterior. Os autores desenvolveram modelos a fim de compreender o comportamento dos fluxos de alimentação e de permeado em processo de separação por membranas que usam a pressão como força motriz, onde esses fluxos são regidos pelas equações de conservação da massa, da quantidade de movimento. WARDEH e MORVAN (2008) usaram o software Ansys-CFX para simular um processo de separação para membranas observando o acúmulo de sais na superfície da membrana comparando seus resultados com o trabalho realizado por FLETCHER e WILEY (2004). AL-OBAIDI e MUJTABA (2016) desenvolveram modelo matemático dinâmico baseado no modelo solução-difusão junto com o mecanismo de concentração-polarização, para membranas de RO, validados com dados da literatura para tratamento de água, sendo investigados efeitos no fluxo de permeado, recuperação, rejeição de sais e pressão. SHIRAZI et al (2016) também mostram diversas pesquisas que utilizam simulações de CFD, aplicadas a processos com membranas, para estudar fenômenos de transferência de movimento, calor e massa em módulos de membranas, com o aperfeiçoamento hidrodinâmico e investigação do efeito de várias geometrias de espaçadores, procurando entender melhor os mecanismos de separação. O objetivo deste trabalho foi empregar a dinâmica dos fluidos computacional (CFD) para avaliar a formação da camada de concentração de sais na superfície de membranas para dessalinização por osmose reversa.

Material e métodos

O modelo matemático usado nas simulações foi de FLETCHER e WILEY (2004) e WARDEH e MORVAN (2008). O esquema da geometria do canal retangular usado nas simulações é ilustrado na Figura 1, com comprimento total de 180 mm e a altura dos canais de alimentação e de permeado de 2 mm e 1,2 mm, respectivamente. Nas simulações, foram adicionadas regiões na entrada e saída foram localizadas em Lin = −20 mm e Lout = 260 mm, para garantir que não haja interferência nos fluxos nas regiões de entrada e saída. Todas as simulações do módulo de membrana foram realizadas usando o pacote Ansys-CFX® 15.0 adotando-se uma solução de NaCl como solução de alimentação com concentração de 2 g/L, fração mássica igual a 0,002. As propriedades físicas e de transporte da solução de NaCl usadas nas simulações, π para pressão osmótica da solução aquosa (Pa), µ é a viscosidade dinâmica (Pa.s), DAB é o coeficiente de difusão de sal na água (m2/s) e ρ é a densidade do fluido (kg/m3), foram as mesmas propostas por GERALDES et al (2001) como função da fração mássica do soluto, válidas para fração mássica de sal de até 0,09. A malha utilizada foi similar à usada por FLETCHER e WILEY (2004) e WARDEH e MORVAN (2008), sendo mais refinada próximo da membrana e se expandindo suavemente para longe da superfície. A etapa seguinte corresponde à definição do modelo matemático baseado nas equações de conservação da massa e de momento, que são as equações que governam os fluxos nos canais de alimentação e de permeado e das condições de contorno. As condições de contorno aplicadas na entrada e saída do canal, paredes e membrana foram as mesmas condições usadas por FLETCHER e WILEY (2004). A velocidade de permeação (vw) é especificada com base na lei de Darcy para meios porosos vw = K(ΔPTM – Δπ), onde ΔPTM é a diferença de pressão transmembranica, Δπ é o diferencial da pressão osmótica através da membrana e K é uma constante baseada no fluxo de permeação do solvente puro. Nas paredes sem membrana, foram aplicadas condições de não deslizamento e sem fluxo de soluto. Na entrada, foi especificado um perfil de velocidade parabólico completamente desenvolvido (u) e uma fração de massa do soluto (mAo). Na saída dos canais a pressão foi configurada considerando os canais abertos para atmosfera p = 0. Os fluxos convectivo e difusivo foram balanceados em ambos os lados da membrana, levando-se em conta que nem todo o soluto permeia através da membrana. No lado de alimentação da membrana, a velocidade tangencial foi ajustada para velocidade nula e a velocidade de permeação (vw), é especificada. No lado do permeado da membrana foram especificados condições similares.

Resultado e discussão

No caso estudado, a velocidade media na entrada foi considerada 0,002 m/s, resultando em um número de Reynolds de 8, determinado com base na velocidade média e da altura do canal. A pressão transmembranica ΔPTM foi 500 kPa. O coeficiente de rejeição R, foi ajustado para 0,95, e o coeficiente, K, para 2x10-10 s−1.Pa−1. Os perfis de velocidade e concentração de soluto através dos canais foram plotados a uma distância de 240 mm da entrada. Os resultados das simulações são apresentados a seguir nas Figuras 2 e 3, mostrando uma concordância entre os resultados obtidos do modelo deste trabalho e os resultados apresentados por FLETCHER e WILEY (2004) e WARDEH e MORVAN (2008). Na Figura 2 está representado o perfil de velocidade axial na direção u nos canais de alimentação e permeado. Observa-se um bom ajuste entre os perfis de velocidade da simulação comparados com os trabalhos de FLETCHER e WILEY (2004) e WARDEH e MORVAN (2008). As simulações foram realizadas para regime permanente, com baixo número de Reynolds (Re = 8) e desprezando-se os efeitos do campo gravitacional, assumindo assim o perfil de velocidade completamente desenvolvido conforme definido como condição de entrada, explicando assim o fato pelo qual as velocidades nos canais de alimentação e de permeado apresentarem um perfil parabólico. O perfil de concentração nos canais de alimentação e de permeado é representado na Figura 3. No lado do canal de alimentação, observa-se que próximo da superfície da membrana ocorre um aumento da concentração de sais presentes na solução salina. Na superfície da membrana a concentração é mais elevada e diminuindo ao se afastar da mesma até atingir o valor da concentração da corrente de alimentação. No lado do canal de permeado, a concentração de sais se manteve baixa e com valores constantes. Esse resultado está conforme esperado no processo de separação que ocorre através de uma membrana semipermeável, onde para esta simulação o índice de rejeição de sais foi ajustado para 95%. Após a análise dos resultados da simulação e comparação com os trabalhos de FLETCHER e WILEY (2004) e WARDEH e MORVAN (2008), foram simulados novos casos, utilizando o mesmo modelo computacional para números de Reynolds iguais a 20, 40, 100 e 200 e para ΔPTM de 600, 700 e 800 kPa. 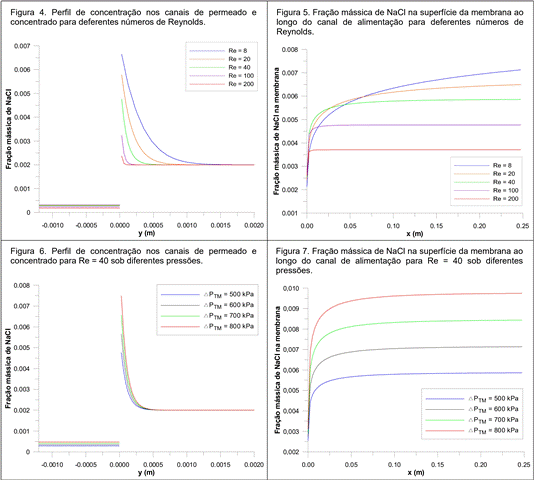A Figura 4 indica o comportamento do perfil de concentração de sais nos canais de permeado e de concentrado em função da altura para os diferentes números e Reynolds. As simulações foram realizadas sob as mesmas condições das simulações anteriores variado apenas número de Reynolds. Os resultados mostram o mesmo comportamento encontrado na figura anterior, próximo à superfície da membrana um aumento da concentração de sais e no canal de permeado uma baixa concentração, resultado do processo de separação promovido pela membrana. Perfis de concentração semelhantes a este são reportados na literatura, como no trabalho de CHANGWEI et al (2015) que realizou um estudo numérico e experimental analisando o efeito da gravidade na performance de um módulo de membrana de RO. O aumento da velocidade na corrente de alimentação provoca um achatamento da altura da camada de concentração próximo da membrana. Na Figura 5 está representada a variação da concentração de sais na superfície da membrana ao longo do canal de alimentação para diferentes números de Reynolds. Pode-se observar que a partir do início da região de permeação da membrana há um aumento significativo da concentração de sais sendo suavizado ao longo do comprimento da membrana. Esse comportamento ocorre devido ao início da permeação de água através da membrana, dessa forma a concentração de sais presentes na corrente de alimentação na região próxima da membrana vai aumentando ao longo do comprimento do módulo. As Figuras 6 e 7 apresentam o comportamento do perfil de concentração de sais nos canais de permeado e de concentrado em função da altura e o perfil de concentração de sais na superfície da membrana, respectivamente. Para esses casos, as simulações foram realizadas com número de Reynolds igual a 40 para diferentes pressões transmembranica. Na Figura 6 observar-se que os perfis de concentração de soluto próximo da membrana apresentam comportamentos semelhantes para diferentes números de Reynolds e reportados na literatura. A variação da concentração de sais na superfície da membrana ao longo do canal de alimentação para diferentes pressões transmembranica está representada na Figura 7. Em todos os casos o comportamento foi semelhante, houve um aumento da concentração de sais no início da região de permeação da membrana até atingir um valor praticamente constante ao longo da membrana, com diferença apenas nos valores. A diferença nos valores das concentrações deve-se ao fato de que com o aumento da pressão transmembranica provoca-se um aumento da permeação de água, diminuindo o volume de água na solução de alimentação deixando-a mais concentrada. Nos projetos de membranas esse comportamento deve ser analisado devido ao fato de que o aumento da concentração junto à superfície da membrana (concentração de polarização) pode provocar incrustações levando ao aumento da pressão transmembranica, provocando uma redução do fluxo de permeado e aumento da passagem de sais, comprometendo o rendimento do sistema de dessalinização, conforme cita KUCERA (2015). As simulações para diferentes números de Reynolds mostraram que variações na velocidade da corrente de alimentação do módulo resultam em alteração da altura da camada de concentração de sais próximo da superfície da membrana, assim como a variação da pressão transmembranica também provoca alteração nesta camada. De acordo com os resultados apresentados, o modelo proposto se mostrou satisfatório a partir da comparação dos resultados da simulação com os resultados obtidos em outros trabalhos com geometria similar, assim como quando submetido a variações da velocidade de alimentação e diferentes pressões. Estes resultados são importantes, pois servem como ponto de partida para a modelagem de outros sistemas de separação por membrana, como cita SCHWINGE et al (2004), o modelo matemático como este pode ser estendido a outras configurações podendo incluir canal de membrana com permeação de dois lados, semelhante ao canal da maior parte dos módulos comerciais que apresentam várias camadas de membrana.

Conclusões

Os resultados das simulações com o modelo usado neste trabalho se mostraram adequado com o objetivo da pesquisa onde foi possível avaliar a formação da camada de concentração de sais na superfície de membranas para dessalinização por RO empregando a fluidodinâmica computacional. Um modelo computacional foi desenvolvido no comercial Ansys-CFX® 15.0, baseado nas equações de conservação de massa, momento linear e de matéria, usando a pressão transmembranica como força motriz para promover o processo de separação. O modelo foi avaliado analisando os perfis de velocidade e concentração de sais nos canais de alimentação e de permeado, em um módulo de membrana alimentado com uma solução de NaCl com concentração de 2 g/L, com baixo número de Reynolds, onde os resultados das simulações mostraram uma boa representatividade dos fenômenos de transferência envolvidos no processo de separação, mostrando concordância com outro modelo de CFD reportado na literatura. Os resultados das simulações com diferentes velocidades da corrente de alimentação (Re = 8, 20, 40, 100 e 200) e diferentes pressão transmembranica (ΔPTM = 500, 600, 700 e 800 kPa) mostraram alterações na camada de concentração de sais próximo da superfície da membrana. O aumento da velocidade na corrente de alimentação provocou uma diminuição da altura da camada de concentração próximo da membrana. Com o aumento da pressão transmembranica houve um aumento da concentração de sais na superfície da membrana devido ao aumento do fluxo de permeação. A aplicação da fluidodinâmica computacional em processos de separação por membranas se mostrou eficaz fornecendo resultados e informações importantes para a análise e entendimento da formação da camada de concentração. Variações em grandezas envolvidas processo, como velocidade e pressão, podem influenciar no desenvolvimento da camada de concentração de polarização.

Agradecimentos

Os autores deste trabalho agradecem a Universidade Federal de Alagoas – Campus Sertão e Universidade Federal de Campina Grande, pelo suporte no desenvolvimento e realização deste trabalho.

Referências

AL-OBAIDE, M. A. & MUJTABA, I. M., Steady state and dynamic modeling of spiral wound wastewater reverse osmosis process. Computers and Chemical Engineering 90: 278-299, 2016.
ANSYS-CFXR 15.0, ANSYS Tutorials, 2013.
BAKER, R.W., Membrane Technology and Applications. John Wiley & Sons Ltd. 2004.
CHANGWEI, H. PERG, K. & SHUGUANG, Z., Experimental and CFD investigation on gravity effectes in reverse osmosis. 45th International Conference on Environmental Systems. Washingotn. 2015.
EL-DESSOUKY, H. T. & ETTOUNEY, H. M., Fundamentals of salt water desalination, Ed. Elsevier, Amsterdam, 2002.
FLETCHER, D. F. & WILEY, D. E., A computational fluid dynamics study of buoyancy effects in reverse osmosis. Journal of Membrane Science 245: 175-181, 2004.
GERALDES, V.M., SEMIAO, V.A. & PINHO, M.N., Flow and mass transfer modelling of nanofiltration. Journal Membrane Science 191: 109-128, 2001.
GHIDOSSI, R., VEYRET, D. & MOULIN, P., Computational fluid dynamics to membranes: State of the art and opportunities. Chemical Engineering and Processing 45: 437-454, 2006.
KUCERA, J., Reverse Osmosis – Design, Processes and Applications for Engineers. Scrivener Publishing LLC. Co-published by John Wiley & Sons, Inc. 2015.
SHIRAZI, M. M. A., KARGARI, A., ISMAIL, A. F. & MATSUURA, T., Computational fluid dynamic (CFD) opportunities applied to the membrane distillation process: state-of-the-art and perspectives. Desalination 377: 73-90, 2016.
SCHNEIDER, R. P., & TSUTIYA, M. T., Membranas filtrantes para o tratamento de água, esgoto e água de reuso. ABES, 1a ed., São Paulo, 2001.
SCHWINGE, J., NEAL, P.R., WILEY, D.E., FLETCHER, D.F. and Fane, A.G., Spiral wound modules and spacers: review and analysis. Journal Membrane Science 242: 129-153, 2004.
WARDEH, S. & MORVAN, H. P., CFD simulations of flow and concentration polarization in spacer-filled channels for application to water desalination. Chemical Engineering Research and Design 86: 1107-1116, 2008.