Diagramas de equilíbrio líquido-líquido e modelagem termodinâmica de sistemas aquosos bifásicos formados PEG 6000 + citrato de sódio + água em diferentes temperaturas

ISBN 978-85-85905-25-5

Área

Química Verde

Autores

Gandolfi, O.R.R. (UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA) ; Gonçalves, G.R.F. (UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA) ; Batista, I.C. (UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA) ; Castro, S.S. (UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA) ; Fontan, R.C.I. (UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA) ; Bonomo, R.C.F. (UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA)

Resumo

Dados de equilíbrio líquido-líquido por sistemas aquosos bifásicos (SABs) compostos por Polietilenoglicol (PEG) 6000 g/mol + citrato de sódio + água em diferentes temperaturas T= (20, 25, 30 e 35) °C foram determinados. Os resultados experimentais dos SABs foram correlacionados utilizando o modelo do Coeficiente de Atividade Funcional Universal (UNIFAC). A temperatura não teve efeito marcante nas curvas binodais, sendo observado apenas um pequeno aumento na região bifásica com o aumento da temperatura. O desvio médio calculado entre as composições experimentais e preditas pelo modelo UNIFAC para os sistemas estudados nas diferentes temperaturas foi de 0,77%. Desta forma, os parâmetros de interação obtidos podem ser utilizados para estimar outros dados de equilíbrio liquido-liquido.

Palavras chaves

UNIFAC; curva binodal; modelagem termodinâmica

Introdução

Sistemas aquosos bifásicos (SABs) são formados espontaneamente após a mistura de duas soluções aquosas de componentes estruturalmente diferentes (como dois polímeros, um polímero e um sal, entre outros), acima de uma concentração crítica, à uma temperatura e pressão específica (AZEVEDO et al., 2009; GONÇALVES et al., 2018). Desde o trabalho pioneiro de Albertsson (1986), vários trabalhos de partição, extração ou purificação de solutos de interesse industrial por sistemas aquosos bifásicos têm sido realizados (GONÇALVES et al., 2018; GÓMES e MACEDO, 2019). A principal vantagem deste método para extração de materiais biológicos é o fato de que as duas fases formadas serem compostas principalmente por água, o que fornece um ambiente favorável à manutenção da estrutura e/ou atividade das biomoléculas (AZEVEDO et al., 2009; BARROS et al., 2014; CHICAROUX e ZEINER, 2019; GÓMES e MACEDO, 2019). Devido as características vantajosas, os SABs têm se tornado objeto de estudo de vários pesquisadores na partição de proteínas, enzimas, ácidos nucleico, corantes, entre outros (BARROS et al., 2016; NASCIMENTO et al., 2018; GÓMES e MACEDO, 2019; ALVARENGA et al., 2015; NAZER et al., 2017). Para a utilização dos SAB no processo de extração é necessário o conhecimento dos diagramas de fase. Para isso, tanto os dados experimentais quanto os modelos termodinâmicos são essenciais (HAMTA et al., 2017). Vários modelos que calculam o valor da energia livre de Gibbs em excesso têm sido propostos para correlacionar os dados de equilíbrio de fase e determinação de coeficientes de atividade. Dentre eles destacam-se os modelos UNIFAC, NRTL, UNIQUAC e ASOG (GEBREYOHANNES et al., 2014; HAMTA et al., 2017; NAZER et al., 2017; DANIELSKI e STRAGEVITCH, 2019). O modelo UNIFAC é um dos mais empregados e utiliza o conceito do método de contribuição de grupo para cálculo do coeficiente de atividade dos componentes presentes na mistura. Neste modelo, os coeficientes de atividade são calculados a partir da contribuição de vários grupos que formam as moléculas do sistema (SMITH et al., 2007). Segundo Perumalsamy e Murugesan, (2009) o método de contribuição de grupos é mais efetivo na predição dos coeficientes de atividade dos componentes em comparação com outros métodos. Entretanto, a eficiência deste método depende da divisão das moléculas em números de grupos que interagem entre si. Neste método a suposição fundamental é que o logaritmo do coeficiente de atividade é assumido como tendo duas contribuições, uma parte combinatorial, devido a diferenças de tamanho e forma das moléculas (entrópica) e uma parte residual, essencialmente devido a interações de energia (entálpica) (FREDENSLUND et al., 1977; PERUMALSAMY e MURUGESAN, 2009; ROBLES et al., 2016). A determinação do coeficiente de atividade é importante na predição de equilíbrio líquido-líquido (Morales et al., 2010). Neste contexto, o objetivo principal deste estudo é a determinação dos diagramas de equilíbrio líquido-líquido dos sistemas formados por polietilenoglicol 6000 + citrato de sódio + água em diferentes temperaturas T = (20, 25, 30 e 35) °C e dos parâmetros de interação entre os grupos de contribuição dos constituintes dos sistemas utilizando o modelo UNIFAC.

Material e métodos

Materiais PEG 6000 g/mol foi obtido da Labsynth produtos para laboratórios Ltda. Citrato de sódio foi obtido da Neon Comercial Reagentes Analíticos Ltda. Foi utilizada água destilada. Determinação dos diagramas de fase Os diagramas de fase foram obtidos pelo método de titulação turbidimétrica de acordo com Albertsson (1986) em diferentes temperaturas T= (20, 25, 30 e 35)°C. A equação empírica não linear proposta por Hu et al., (2004) foi utilizada e correlacionada aos dados experimentais de cada binodal obtida, utilizando o software SigmaPlot v.11.0 Foram determinados 3 linhas de amarração para cada diagrama de equilíbrio de fase, utilizando o método gravimétrico descrito por Merchuk et al. (1998). As concentrações de cada componente nas fases coletadas foram determinadas pela regra da alavanca através da resolução de um sistema de quatro equações e quatro incógnitas, utilizando o solver do Excel. Todos os sistemas foram preparados em duplicata (Nascimento et al., 2018; Pimentel et al., 2017). Modelagem termodinâmica Para determinação dos parâmetros de interação entre os grupos de contribuição dos componentes do sistema foi utilizado o modelo UNIFAC (Fredenslund et al., 1977) com a abordagem de Kikic et al. (1991). O modelo UNIFAC original considera o coeficiente de atividade como sendo a soma de um termo combinatorial (devido as diferenças de tamanho e forma das moléculas (entrópica)) e um termo residual (devido as interações de energia (entálpica)). A abordagem de Kikic et al. (1991) adiciona um termo referente as interações de logo alcance no coeficiente de atividade, dada pela teoria de Debey-Huckel (Barreto et al., 2019; Nascimento et al., 2018). Os dados experimentais de equilíbrio líquido-líquido foram utilizados para estimar os parâmetros de interação dos grupos de contribuição através do modelo UNIFAC implementado no código Fortran TML-LLE 2.0 (AZNAR et al., 1998). O método consiste na minimização da função objetivo (Nascimento et al., 2018; Batista et al., 2019). Com os parâmetros de interação estimados pelo método, a comparação entre os valores preditos e experimentais de cada componente em cada uma das fases foi realizada através da raiz quadrada do desvio médio (δx)(Nascimento et al., 2018; Batista et al., 2019).

Resultado e discussão

Os diagramas de equilíbrio para os sistemas formados por PEG 6000 + citrato de sódio + água foram obtidos em diferentes temperaturas T= (20, 25, 30 e 35) °C. Esses diagramas fornecem informações sobre as concentrações dos componentes necessárias para a formação das duas fases. Quanto mais a curva se aproxima da origem, menor a concentração de PEG e sal necessária para formar o SAB. Abaixo das curvas obtidas para cada condição estudada de temperatura, tipo de sal ou massa molar do polímero, a mistura dos constituintes do sistema encontra-se miscível, formando uma fase homogêneas, enquanto acima das curvas verifica-se a formação de duas fases (IQBAL et al., 2016). A formação de SAB resulta do processo de exclusão mútua entre o sal e o polímero, visto que ambos apresentam alta afinidade com a molécula de água. Sob pressão e temperatura constante, acima de uma concentração crítica, a extensão de exclusão aumenta, fazendo com que a fase inferior concentre em sal e a fase superior em polímero (DA SILVA et al., 2008; MURARI et al., 2015). Esse processo de segregação ocorre devido às interações mais favoráveis ocorrerem entre componentes similares (sal-sal e polímero- polímero) (PATRÍCIO et al., 2011). Para todos os sistemas estudados, a temperatura não teve efeito marcante nas composições de equilíbrio de fase dos SABs, sendo observado apenas um pequeno aumento na região bifásica com o aumento da temperatura. O aumento da região bifásica promovido pelo aumento da temperatura de equilíbrio é uma indicação de que o processo de separação de fases é endotérmico e concorda com a ideia de que a formação do SAB é entropicamente dirigida (RENGIFO et al., 2016). Essa característica entrópica do processo de separação de fases é uma característica geral dos sistemas aquosos bifásicos, como descrito por vários autores (MURARI et al., 2015; NASCIMENTO et al., 2018). Comportamento similar foi encontrado por Nascimento et al. (2018) que estudaram dados de equilíbrio de sistemas aquosos bifásicos composto por PEG 1500 + citrato de sódio + água, em diferentes temperaturas (30, e 40) °C e valores de pH (4, 5, 6, e 7). Mesmo a temperatura não apresentando um efeito marcante nos diagramas de equilíbrio, é possível que apresente efeito sobre as linhas de amarração (Comprimento e inclinação das linhas de amarração) e consequentemente na partição do soluto nos SABs, visto que com o aumento da temperatura ocorre maior mobilidade das moléculas do sistema. Os dados de equilíbrio líquido-líquido determinados nas diferentes temperaturas foram ajustados a equação proposta por Hu et al., (2004). T=20°C: w₁=exp(1,513−23,230*(w₂) ²₊61,384*w₂−221,288*(w₂)²). R²=0,999. T=25°C: w₁=exp(−0,382−4,767*(w₂) ²₊3,726*w₂− 90,567*(w₂)²). R²=0,999. T=30°C: w₁=exp(−0,381−3,541*(w₂)² −1,227*w₂−93,729*(w₂) ²). R²=0,998. T=35°C: w₁=exp(−0,325−5,332*(w₂) ²₊12,658*w₂−193,765*(w₂)²). R²=0,998. Com base nos valores de R² pode-se verificar que o modelo se ajustou de forma satisfatória aos dados experimentais. Os valores dos parâmetros a, b, c e d foram utilizados para estimar as composições dos componentes da fase superior e inferior pela regra da alavanca. 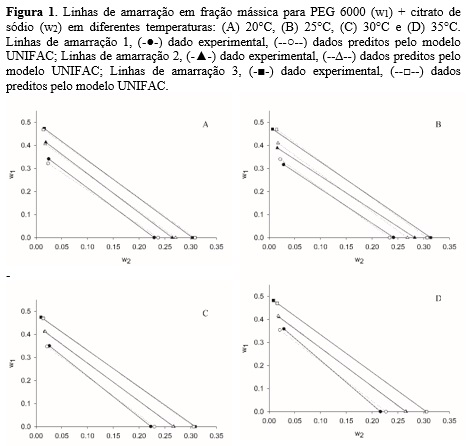Pode-se observar na figura 1 as composições de equilíbrio para os sistemas estudados em diferentes temperaturas, expressas em fração mássica, obtidos pela regra da alavanca. Estimativa dos parâmetros de interação Para esta estimativa dos parâmetros de interação de grupo foram necessários parâmetros de volume (R_K) e área (Q_K)), já descritos na literatura, como observado por Andrade et al., (2011) Magnussen et al., (1981), Mols e Gmehling (2013), Ninni et al., (1999) e Weast (1972). 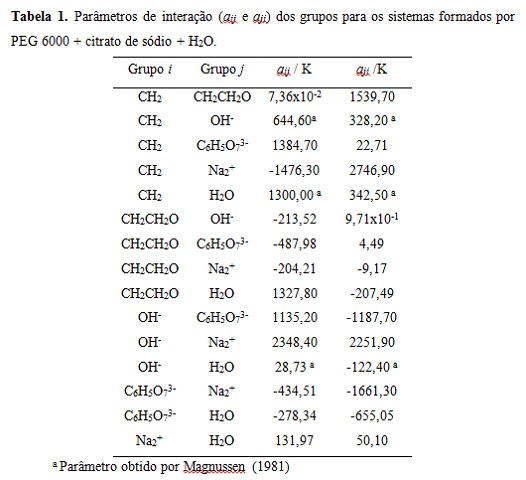Na Tabela 1 estão apresentados os parâmetros de interação aij e aji obtidos na literatura, bem como os parâmetros de interação estimados entre os grupos. Tais parâmetros foram obtidos utilizando as três linhas de amarração e as diferentes temperaturas estudadas T= (20, 25, 30 e 35) °C. O desvio médio calculado para os sistemas foi de 0,77%. Tal resultado mostra que o desvio médio geral foi muito baixo, mostrando uma excelente representação para os sistemas analisados. De acordo com este resultado, os parâmetros de interação obtidos entre os grupos de contribuição podem ser utilizados para estimar outros dados de equilíbrio liquido-liquido. As composições das fases foram estimadas pelo modelo UNIFAC a partir dos parâmetros de interação e comparadas com as composições experimentais, como mostrado na figura 1. Como pode-se observar na figura 1 que os dados calculados praticamente se sobrepões aos experimentais, mostrando que o modelo utilizado foi adequado para os sistemas estudados

Conclusões

Foram obtidos dados de equilíbrio de sistemas compostos por polietilenoglicol 6000, citrato de sódio e água em diferentes temperaturas T = (20, 25, 30 e 35) °C, onde foi verificado que a temperatura não apresentou grande efeito nos diagramas de equilíbrio. Foram determinados 3 linhas de amarração para cada sistema estudado. Foram obtidos parâmetros de interação entre os grupos de contribuição dos componentes dos sistemas, pelo modelo UNIFAC. Os resultados obtidos pelo modelo termodinâmico são adequados e os modelo UNIFAC apresentou excelentes resultados com baixos desvios entre as composições experimentais e calculadas. Desta forma, tais parâmetros de interação podem ser utilizados para estimar outros dados de equilíbrio liquido-liquido.

Agradecimentos

Os autores agradecem o apoio financeiro da FAPESB.

Referências

ALBERTSSON, P.A. Partition of cell and macromolecules. New York: John Wiley, 1986, 346p.
ALVARENGA, J. M.; FIDELES, A. R.; DA SILVA, M. V.; MURARI, G. F.; TAYLOR, J. G.; DE LEMOS, L. R.; RODRIGUES, G. D.; MAGESTE, A. B. Partition study of textile dye Remazol Yellow Gold RNL in aqueous two-phase systems. Fluid Phase Equilibria, v. 391, p. 1-8, 2015.
ANDRADE, V. M.; RODRIGUES, G. D.; CARVALHO, R. M. M.; DA SILVA, L. H. M.; DA SILVA, M. C. H. Aqueous two-phase systems of copolymer L64 + organic salt + water: Enthalpic L64–salt interaction and Othmer–Tobias, NRTL and UNIFAC thermodynamic modeling. Chemical Engineering Journal, v. 171, p. 9-15, 2011.
AZEVEDO, A. M.; ROSA, P. A. J.; FERREIRA, I. F.; AIRES-BARROS, M. R. Chromatography-free recovery of biopharmaceuticals through aqueous two-phase processing. Trends in Biotechnology, v. 27, p. 240-247, 2009.
AZNAR, M.; STRAGEVITCH, L.; DAVILA, S. G. Liquid-liquid equilibria: a comparison between original and modified UNIFAC, Latin American Applied Research, v. 28 p. 135-138, 1998.
BARRETO, C. L. R.; CASTRO, S. S.; JÚNIOR, E. C. S.; VELOSO, C. M.; VERÍSSIMO, L. A. A.; SAMPAIO, V. S.; GANDOLFI, O. R. R.; FONTAN, R. C. I.; NEVES, I. C. O.; BONOMO, R. C. F. Liquid−Liquid Equilibrium Data and Thermodynamic Modeling for Aqueous Two-Phase System Peg 1500 + Sodium Sulfate + Water at Different Temperatures. Journal of Chemical and Engineering Data, v. 64, p. 810-816, 2019.
BARROS, D. P. C. CAMPOS, S. R. R.; MADEIRA, P. P.; AZEVEDO, A. M. BATISTA, A. M.; AIRES-BARROS, M. R. Modeling the partitioning of amino acids in aqueous two-phase systems. Journal of Chromatography A, v. 1329, p. 52-60, 2014.
BARROS, D. P. C.; CAMPOS, S. R. R.; AZEVEDO, A. M.; BATISTA, A. M.; AIRES-BARROS, M. R. Predicting protein partition coefficients in aqueous two-phase system. Journal of Chromatography A, v. 1470, p. 50-58, 2016.
CHICAROUX, A. K.; ZEINER, T. Theoretical and experimental investigation of mass transfer in aqueous two-phase systems based on linear and branched polymers. Fluid Phase Equilibria, v. 479, p. 106-113, 2019.
DA SILVA, L. H. M.; DA SILVA, M. C. H.; FRANCISCO, K. R.; CARDOSO, M. V.; MINIM, L. A.; COIMBRA, J. S. R. PEO-[M(CN)5NO]x- (M = Fe, Mn, or Cr) Interaction as a Driving Force in the Partitioning of the Pentacyanonitrosylmetallate Anion in ATPS: Strong Effect of the Central Atom. The Journal of Physical Chemistry B, v. 112, p. 11669-11678, 2008.
DANIELSKI, L.; STRAGETICH, L. Cap. 4: Classical Models Part 2: Activity Coefficient Models and Applications. Thermodynamics of Phase Equilibria in Food Engineering, p. 103-162, 2019.
FREDENSLUND, GMEHLING J, RASMUSSEN P. Vapor-liquid equilibrium using UNIFAC. Amsterdam: Elsevier; 1977.
GEBREYOHANNES, S.; NEELY, B. J.; GASEM, K. A. M. One-parameter modified nonrandom two-liquid (NRTL) activity coefficient model. Fluid Phase Equilibria, v. 379, p. 196-205, 2014.
GÓMES, E.; MACEDO, E. A. Partitioning of DNP-amino acids in ionic liquid/citrate salt based Aqueous Two-Phase System. Fluid Phase Equilibria, v. 484, p. 82-87, 2019.
GONÇALVES, L. F. S.; FELIZBERTO, N. C. M.; SILVA, K. C.; MAGISTA, A. M.; RODRIGUES, G. D.; LEMOS, L. R. Equilibrium phase behavior of aqueous two-phase system formed by triblock copolymer + sulfate salt + water at different temperatures. Fluid Phase Equilibria, v. 479, p. 145-152, 2018.
HAMTA, A. DEHGHANI, M. R.; GHOLAMI, M. Novel experimental data on aqueous two–phase system containing PEG–6000 and Na2CO3 at T = (293.15, 303.15 and 313.15) K. Journal of Molecular Liquids, v. 241, p. 144-149, 2017.
IQBAL, M.; TAO, Y.; XIE, S.; ZHU, Y.; CHEN, D.; WANG, X.; HUANG, L.; PENG, D.; SATTAR, A.; SHABBIR, M. A. B.; HUSSAIN, H. I.; AHMED, S.; YUAN, Z. Aqueous two-phase system (ATPS): an overview and advances in its applications. Biological Precedures Online, v. 18, p. 18, 2016.
KIKIC, I.; FERMEGLIA, M.; RASMUSSEN, P. UNIFAC prediction of vapor-liquid equilibria in mixed solvent-salt systems. Chemical Engineering Science, v. 46, p. 2775-2780, 1991.
MAGNUSSEN, T.; RASMUSSEN, P.; FREDENSLUND, A. UNIFAC parameter table for prediction of liquid-liquid equilibriums. Industrial and Engineering Chemistry Process Design and Development, v. 20, p. 331-339, 1981.
MERCHUK, J. C., ANDREWS, B. A., ASENJO, J. A., Aqueous two-phase systems for protein separation. Studies on phase inversion, Journal Chromatography B, v. 711, p. 285293, 1998.
MOLS, A.; GMEHLING, J. A revised LIQUAC and LIFAC model (LIQUAC*/LIFAC*) for the prediction of properties of electrolyte containing solutions. Fluid Phase Equilibria, v. 337, p. 311-322, 2013.
MURARI, G. F.; PENIDO, J. A.; MACHADO, P. A. L.; LEMOS, L. R.; LEMES, N. H. T.; VIRTUOSO, L. S.; RODRIGUES, G. D.; MAGESTE, A. B. Phase diagrams of aqueous two-phase systems formed by polyethylene glycol + ammonium sulfate + water: equilibrium data and thermodynamic modeling. Fluid Phase Equilibria, v. 406, p. 61-69, 2015.
NASCIMENTO, M. B.; CASTRO, S. S.; VELOSO, C. M.; FONTAN, R. C. I.; NASCIMENTO, D. J.; GANDOLFI, O. R. R.; SAMPAIO, V. S.; VERÍSSIMO, L. A. A.; BONOMO, R. C. F. Equilibrium data and thermodynamic studies of α-amylase partition in aqueous two-phase systems. Fluid Phase Equilibria, v. 463, p.69-79, 2018.
NAZER, B.; DEHGHANI, M.; GOLIAEI, B.; MORAD, E. Partitioning of pyrimidine single stranded oligonucleotide using polyethylene glycol e sodium sulfate aqueous two-phase systems; experimental and modeling. Fluid Phase Equilibria, v. 432, p. 45-53, 2017.
NINNI, L.; CAMARGO, M. S.; MEIRELLES, A. J. A. Water activity in poly(ethylene glycol) aqueous solutions. Thermochimica Acta, v. 328, p. 169-176, 1999.
PATRÍCIO, P. R.; MAGESTE, A. B.; LEMOS, L. R.; CARVALHO, R. M. M.; DA SILVA, L. H. M.; DA SILVA, M. C. H. Phase diagram and thermodynamic modeling of PEO + organic salts +H2O and PPO + organic salts +H2O aqueous two-phase systems. Fluid Phase Equilibria, v. 305, p. 1-8, 2011.
PERUMALSAMY, M.; MURUGESAN, T. Prediction of liquid–liquid equilibria for polyethylene glycol based aqueous two-phase system by ASOG and UNIFAC method. Brazilian Journal of Chemical Engineering, v. 26, p. 171-180, 2009.
PIMENTEL, J. G.; BICALHO, S. F.; GANDOLFI, O. R. R.; VERRÍSIMO, L. A. A.; CASTRO, S. S.; SOUZA, E. A.; VELOSO, C. M.; FONTAN, R. C. I.; SAMPAIO, V. S.; BONOMO, R. C. F. Evaluation of salting-out effect in the liquid–liquid equilibrium of aqueous two-phase systems composed of 2-propanol and Na2SO4/MgSO4 at different temperatures. Fluid Phase Equilibria, v. 450, p. 84-193, 2017.
RENGIFO, A. F. C.; FERREIRA, G. M. D.; FERREIRA, G. M. D.; DA SILVA, M. C. H.; REZENDE, J. P.; PIRES, A. C. S.; DA SILVA, L. H. M. Driving forces for chymosin partitioning on the macromolecule-salt aqueous two-phase system. Food and Bioproducts Processing, v. 100, p. 361-371, 2016.
SMITH, J. M.; VAN NESS, H. C.; ABBOTT, M. M. Introdução à Termodinâmica da Engenharia Química, 7ª Ed. Editora LTC, 2007.
WEAST, R. C. Handbook of Chemistry and Physics. 53rd ed.; Chemical Rubber Co.: 1972.