PROPOSTA DIDÁTICA PARA O ENSINO DO MOL A PARTIR DA DETERMINAÇÃO DA CONSTANTE DE AVOGADRO EM COMPOSTOS IÔNICOS CRISTALINOS

ISBN 978-85-85905-25-5

Área

Ensino de Química

Autores

Vasconcelos, S.J.T. (INSTITUTO FEDERAL DO CEARÁ)

Resumo

O presente trabalho apresenta um breve levantamento bibliográfico e uma proposta metodológica para o cálculo da constante de Avogadro (NA) a partir desta, a discussão sobre mol e quantidade de matéria. O tema é atual e precisa ser reinventado devido à recente redefinição de mol no SI. Para o cálculo da constante propõe-se o uso de conceitos básicos de cristalografia aplicado a compostos iônicos sólidos, com os quais efetivamente pode se calcular NA empregando uma formulação matemática simples. Destaca-se que a inclusão destas informações no currículo escolar pode ser um importante fator interdisciplinar. Fez-se a determinação da constante para quatro compostos iônicos, chegando-se a valores bem próximos de NA, a depender de quais informações foram utilizadas e de qual composto analisado.

Palavras chaves

Redefinição de mol; Constante de Avogadro; Proposta didática

Introdução

Desde janeiro de 2018 a IUPAC recomenda o uso da definição da unidade mol baseada apenas no valor da constante de Avogadro[1]. A definição anterior tornou-se ultrapassada devido a sua dependência com a massa que por sua vez estava associada a um protótipo que perdera a confiança com o tempo [2]. A antiga definição também estava diretamente associada a uma substância específica e, embora indicasse a existência de uma constante (a constante de Avogadro – NA) não a explicitava. O valor aproximado desta constante largamente utilizado era NA = 6,022 x 10^23 mol-1. Contudo, o avanço tecnológico e a precisão cada vez maior das medidas permite calcular o valor exato de NA[3]. A obtenção do valor exato de NA esteve no centro de uma discussão que durou mais de uma década e resultou em 2015 na determinação do seu valor exato de 6,02214076 x 10^23[4]. Empregou-se a difração de raios-X numa esfera cristalina de 28Si quase perfeita para determinar a quantidade de átomos presentes. A mudança conceitual foi significativa e exige que os docentes esclareçam que o mol não tem relação com nenhuma substância química específica, sendo seu valor unitário igual ao próprio número de Avogadro. O presente trabalho busca transformar esta dificuldade em oportunidade de contextualização do ensino. O 28Si foi escolhido pelo fato de possuir estrutura cristalina conhecida com células do tipo cúbicas, que facilitam os cálculos. Por meio da difração de raios-X permite determinar a cristalinidade dos materiais sólidos [5]. Sólidos iônicos com células unitárias cúbicas são uma alternativa para o cálculo de NA que pode ser utilizado como recurso didático interdisciplinar. Existem duas possibilidades de redes cristalinas cúbicas para compostos iônicos: a rede cúbica de corpo centrado (CCC) e a rede cúbica de faces centrada (CFC)[6]. Nas redes CCC e CFC ocorrem íons, além dos vértices, no centro e nas arestas do cubo, respectivamente. Quantos íons e íons-fórmula comporta cada célula unitária cúbico? É fácil demonstrar que numa célula CCC o número de fórmulas por célula (nf) é 1, enquanto que numa CFC, nf = 4. Este valor é essencial para os cálculos posteriores. Para um composto iônico AB com célula do tipo CCC, tem-se que o comprimento da célula (a) é aproximadamente: a(ccc) = 2r(B) {1} onde r(B) é o raio iônico de B. Já para uma célula CFC a(cfc) = 2.[r(A) + r(B)] {2} contudo, há um erro considerável nessas aproximações, sendo a melhor opção recorrer a valores cristalográficos obtidos por difração de raios-X.Conhecendo o valor de a, o volume da célula (Vc) é dado por: Vc = a^3 {3} O valor de Vc é fundamental para o cálculo que será realizado.

Material e métodos

A principal conclusão que podemos tirar da antiga definição de mol é que a massa de uma substância em gramas numericamente igual a sua massa molar contém exatamente 1 mol de entidades. A primeira etapa desta metodologia consistiu na escolha das substâncias sólidas cristalinas. No presente trabalho, empregou-se os compostos iônicos NaCl, MgO, CsCl e RbF. Para o cálculo de a e Va por meio de cálculo geométrico da célula unitária empregou-se dados de raio iônico disponíveis na literatura[7]. Já os dados cristalográficos da difração de raios-X que também resultaram nos valores de a e Va foram obtidos a partir do Inorganic Crystal Structure Database[8]. Valores de massa molar e densidade também foram obtidos diretamente da literatura. De posse das informações, partiu-se para a determinação da expressão matemática resolutiva. Ao se dividir o volume de uma amostra sólida (Va) pelo volume de uma de suas células unitárias (Va) obtém-se o número de células unitárias (nc) presentes na amostra. Então: nc = Va/Vc {4} Como a massa específica da amostra (p) é dada por p = ma/Va {5} tem-se que Va = ma/p {6} Substituindo {6} em {4}, tem-se: nc = ma/(p.Va) {7} Quando a massa do sólido for numericamente igual a sua massa molar (ma = MM), temos que nc indica o numero de células em 1 mol de amostra. Ao multiplicar pelo número de fórmulas por célula unitária (isto é, nf), obtemos o número de fórmulas por 1 mol de amostra, o que corresponde ao próprio valor de NA. Ou seja: NA = (MM.nf)/(p.Vc) {8} que é a expressão matemática resolutiva do problema. Uma vez deduzida, a expressão foi aplicada para os compostos citados considerando-se duas formas de cálculo. Na primeira, o valor de Vc foi obtido a partir dos raios iônicos e os valores de p foram retirados da literatura. No segundo caso, os valores de Vc e p foram obtidos a partir dos dados de difração de raios-X disponíveis no banco de dados do ICSD. Os resultados obtidos foram reunidos e comparados entre si, objetivando estabelecer os que se aproximaram mais do valor correto de NA. A proposta é empregar o cálculo de NA como ferramenta de ensino para o conceito de mol e demonstrar como um cálculo semelhante ao realizado pela IUPAC pode ser feito empregando-se dados da literatura. Mais que isso, pretende-se mostrar como diversos assuntos da Física e Química estão interligando e como estes podem ser utilizados para mais que uma demonstração, mas sobretudo, para o ensino de um conceito tão fundamental em Química como o mol.

Resultado e discussão

A Figura 1 reúne os dados para as substâncias NaCl, MgO, CsCl e RbF. Com estes dados realizou-se os cálculos de NA empregando dois métodos: o que se chamou de "geométrico" partiu dos valores dos raios iônicos da literatura para obter o valor de Vc e assim, calcular NA. Já o método chamado de "cristalográfico" partiu dos valores de a das células unitárias dos compostos. O valor de NA calculado para cada compostos por cada método está indicado na Figura 2. A seguir demonstra-se como cada cálculo foi realizado para o NaCl. Para obtenção de NA pelo método geométrico, aplicou-se equação {2}: a = 2.(102 pm+181 pm) = 566 pm. Sendo conveniente empregar a unidade cm (sendo 1m = 10^2 cm), temos que: 566 pm = 566 x 10^-12 m = 566 x 10^-12 x 10^2 = 566 x 10^-10 cm). De posse deste resultado, Vc foi obtido através da equação {3}: Vc = (566 x 10^-10 cm)^3 = 1,8132 x 10-22 cm^3, conforme está na figura 1. Os demais valores foram retirados da figura 1. Finalmente, aplicando equação {8}, tem-se: NA = (58,443 x 4)/(2,15 x 1,8132 x 10^-22) = 6,000 x 10 ^23. Empregando-se os dados cristalográficos e efetuando o cálculo por meio da equação {8}, tem-se: NA = (58,443 x 4)/(2,39 x 1,619 x 10^-22) = 6,042 x 10 ^23. Nota-se como o valor obtido com os dados cristalográficos se aproximam mais do valor exato atualmente atribuído a constante. Repetindo os cálculos realizados anteriormente para todos os compostos empregando as duas metodologias de cálculos, obteve-se os valores de NA listados na Figura 2. Observa-se uma divergência significativa entre os valores obtidos a partir daqueles obtidos a partir dos raios iônicos (método "geométrico") e os de cristalografia. Os dados de cristalografia fornecem valores muito mais precisos, independente do tipo de célula unitária do composto analisado, diferentemente do método geométrico, onde as células do tipo CFC fornecem valores bem mais próximos. PROPOSTA DIDÁTICA A proposta didática baseia-se na abordagem interdisciplinar do conteúdo. Não se propõe que o cálculo da constante seja o mais importante, mas este demonstra como o valor, em si, pode ser obtido empregando-se os mesmos princípios que foram utilizados para a determinação oficial de NA. O primeiro aspecto que deve ser abordado é o histórico, demonstrando como o estabelecimento das grandezas e unidades do SI foram em consequência direta da necessidade científica, tecnológico e comercial, tendo demandado um longo tempo. Depois, pode-se destacar o quanto é importante a existência do sistema para o mundo científico e tecnológico moderno e, também, o quanto o desenvolvimento de novas tecnologias depende da existência de métodos extremamente precisos de medição. Destacado isto, o professor pode então, ater-se mais a Química e a unidade mol (seu objeto de ensino), introduzindo-a da forma como julgar melhor, mas ressaltando sua relação com a constante de Avogadro. Deste ponto em diante, o cálculo de NA passa a ganhar destaque, segundo a metodologia proposta neste trabalho. Recomenda-se ao professor a não mostrar o valor da constante e sim, estimular os estudantes para que estes a calculem. Sugere-se um trabalho em equipe na qual, cada equipe trabalhe com um composto iônico, que podem ser os listados neste trabalho, ou outros que o professor preferir (como vimos, os compostos iônicos de célula CFC fornecem valores mais precisos). Neste momento, é importantíssimo que o professor revise conceitos de ligações iônicas e explique minimante como como funciona a difração de raios-X e o significa termos como raio iônico, comprimento da célula (parâmetro de rede), etc. Sugere-se que cada equipe monte sua tabela de dados (a tabela mostrada na figura 1 deste trabalho) por consulta a uma lista de raios iônicos para o seu composto e o professor forneça os dados cristalográficos, visto que estes são de mais difícil acesso. Quanto a equação resolutiva (equação {8}), esta pode ser deduzida pelo professor durante as explicações prévias do trabalho, com esclarecimento do significado de cada um dos seus termos. Após isto, as equipes podem calcular seu próprio valor de NA. O professor deve estar atento à forma como estes calculam, tendo em vista que erros matemáticos comuns poderem ocorrer. É importante que cada equipe calcule NA usando cada método, para que os próprios estudantes possam comparar os valores. Feito isto, cada equipe deve expor seus resultados para os demais e a forma como os mesmos foram calculados. Importante também cada equipe explicitar em qual etapa sentiu mais dificuldade (se no cálculo ou no entendimento do que o cálculo representava, por exemplo). O professor deve reunir os valores encontrados por cada equipe para cada composto e deixar exposto para que toda a turma veja as diferenças. Finalmente, o professor mostra o valor exato da constante de Avogadro e compara aos valores obtidos pelos estudantes. Deve ainda questionar o porque dos valores divergentes (fazendo associações com o fator de empacotamento ou ionicidade do composto). Para finalizar, é de suma importância que o professor mostre como os cálculos oficiais foram feitos, mostrando o trabalho de Azuma Azuma, Y. et al.[4] que calculou o valor exato de NA. O professor deve mostrar que os estudantes empregaram a mesma equação que os cientistas e que a única diferença entre o cálculo "correto" e a aproximação dos estudantes deveu-se apenas à precisão dos dados empregados por cada um desses grupos, e não ao método em si. Esta discussão é importantíssima, pois fará com que os estudantes cheguem a duas conclusões: primeiro, que a precisão das medidas é fundamental (isso só reforça a existência do SI e sua importância) e segundo, o método do cálculo de NA é simples e pode ser replicado com relativa facilidade, fazendo com que eles percebam que este conceito é, em sua essência, muito simples. Para finalizar, o professor deve realizar uma breve avaliação da atividade realizada, que pode ser qualitativa ou quantitativa. Esta pode ou não valer pontos, mas seu objetivo é fixar o que foi aprendido. Os estudantes, podem, por exemplo, calcular a massa em gramas do composto de sua equipe que contenha o dobro ou o triplo de mols equivalente a 1 NA; ou descrever como eles acham que é possível utilizar um número tão grande na Química ou, ainda, o que significa o valor de 1 NA. Acredita-se que esta atividade possa ser realizada no tempo máximo de duas horas (equivalente a duas aulas consecutivas). Contudo, caso não seja possível, o professor pode aproveitar um eventual intervalo de dias entre o início e o fim da atividade para solicitar que as equipes façam uma pesquisa sobre algum aspecto do assunto que, pode, inclusive, figurar como uma avaliação. Ao final desta, o professor pode fazer seu encerramento como preferir, já ressaltando que mol e NA serão objetos de estudo dali em diante e que muitas aplicações serão vistas a partir da aula seguinte.

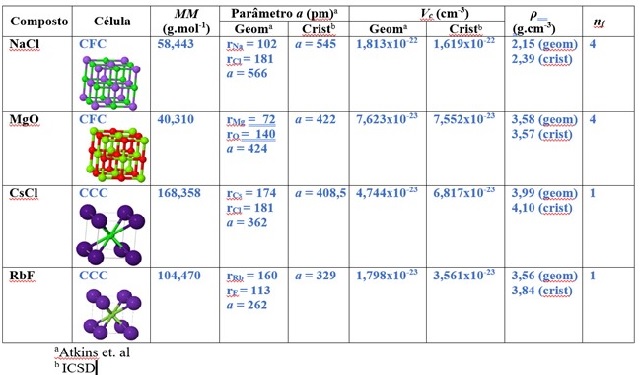
Dados utilizados para cálculo de NA: valores assinalados como "geom" são literatura e os assinalados como "crist" são dados da cristalografia.


Resultados do cálculo de NA obtidos pelos dados da literatura e pelos dados de cristalografia.

Conclusões

O presente trabalho trouxe uma discussão ainda ausente no Brasil. Destacamos a importância desta discussão que é, além de recente, determinante para a compreensão de diversos outros temas ligados à Química. Portanto, é de extra importância o estabelecimento de novas propostas metodológicas para o ensino de qualquer temática, especialmente as mais fundamentais, como o conceito de mol. A metodologia proposta pretende ser eficiente e relativamente simples para a demonstração do cálculo de NA a partir de sólidos cristalinos, especialmente, os iônicos. Ressalta-se que o cálculo da citada constante a partir da cristalografia de sólidos (28Si, no caso) é a abordagem atualmente aceita pela IUPAC. Além da dedução de uma expressão matemática útil e amplamente aplicável, demonstrou-se como o cálculo é feito para compostos iônicos com uma precisão relativamente alta para compostos com células do tipo CFC quando empregados dados de raios iônicos da literatura. Já os cálculos empregando valores de cristalografia são muito mais precisos, independente da célula unitária do sólido. Partindo dos raios iônicos, os valores de NA tendem a divergir muito para células do tipo CCC devido, sobretudo, ao menor fator de empacotamento deste sistema cristalino. A proposta didática prevê um trabalho de equipe entre os estudantes em sala de aula, objetivando obter os dados da literatura e o cálculo do valor de NA. Segue-se uma discussão dos resultados e justificativas por parte das equipes. Ressalta-se que os docentes ainda podem enriquecer enormemente a discussão incluindo temas como ligações químicas e formação de compostos iônicos, outros tipos de células unitárias, bem como uma discussão introdutória sobre o funcionamento da técnica de difração de raios-X, além da própria discussão sobre a radiação, em si. Por fim, destacamos que a metodologia proposta deve ser executada para a verificação de sua aplicabilidade e efeitos práticos, aspectos que figuram como perspectivas deste trabalho.

Agradecimentos

O autor agradece a Universidade Federal do Ceará (UFC) pelo acesso ao banco de dados cristalográfico através do acesso via DotLib (https://bdec.dotlib.com.br) e ao Instituto Federal do Ceará pela disponibilização do servidor.

Referências

[1] BIPM. Proceedings of the 23rd meeting of the General Conference on Weights and Measures, Paris, 2007.
[2] Davis, R. The SI unit of mass. Metrologia, n. 40, p. 299–305, 2003.
[3] Marquardt, R. et al. Definition of the mole (IUPAC Recommendation 2017). Pure Appl. Chem., n. 90, p. 175–180, 2018.
[4] Azuma, Y. et al. Improved measurement results for the Avogadro constant using a 28Si-enriched crystal. Metrologia, n. 52, p. 360–375, 2015.
[5] Callister Jr., W. D. Ciência e engenharia de materiais: uma introdução. 7 ed. Rio de Janeiro: LTC, 2008.
[6] Kittel, C. Introdução à Física do estado sólido. 8 ed. Rio de Janeiro: LTC, 2006.
[7] Atkins, P. W. et al. Shriver and Atkin’s Inorganic Chemistry, 5 ed. New York, W. H. Freeman and Company, 2010.
[8] Inorganic Crystal Structure Database. Disponível em: <https://icsd.products.fiz-karlsruhe.de/> Acesso: 15/08/2019.