Solução computacional do modelo de Gouy-Chapman-Stern para a dupla camada elétrica.

ISBN 978-85-85905-25-5

Área

Físico-Química

Autores

de Moraes, A.S. (UNIVERSIDADE ESTADUAL DO CENTRO-OESTE) ; Lopes, M.C. (UNIVERSIDADE ESTADUAL DO CENTRO-OESTE)

Resumo

Neste trabalho propomos um modelo computacional, baseado na teoria de Gouy- Chapman Stern, para estudar o comportamento da dupla camada elétrica em uma interface metal/solução, usando o software COMSOL Multiphysics. Utilizamos uma geometria simplificada, unidimensional, a fim de poder comparar as soluções numéricas com as soluções analíticas conhecidas e, deste modo, testar a validade do modelo e a adequação do software. Foram calculados a carga superficial e a capacitância em função do potencial elétrico do metal bem como os perfis de potencial e concentração na solução. Os resultados mostraram que, mediante ajuste adequado da malha de cálculo, as soluções numéricas são suficientemente exatas e sugerem que o modelo pode ser estendido para a modelagem de supercapacitores.

Palavras chaves

dupla camada elétrica; Simulação computacional; Eletroquímica

Introdução

Neste trabalho apresentamos a solução computacional do modelo de Gouy- Chapman-Stern para a dupla camada elétrica formada por um eletrodo metálico imerso em uma solução eletrolítica, utilizando o software COMSOL Multiphysics. Este modelo clássico é a base teórica para a compreensão da estrutura da dupla camada elétrica e sua influência nos sistemas eletroquímicos. A sua solução computacional é importante em diferentes aspectos: i) permite validar o método computacional através da comparação de resultados numéricos com a solução analítica conhecida; ii) uma vez validado o método, permite explorar condições para as quais a solução analítica não existe, mas são importantes tecnologicamente, como, por exemplo, eletrodos porosos utilizados em supercapacitores; iii) permite explorar hipóteses teóricas a fim desenvolver modelos mais adequados, como por exemplo a variação da constante dielétrica da água próxima ao eletrodo; iv) facilita a compreensão e apresentação do modelo, podendo ser utilizado no ensino de eletroquímica. Até onde vai o conhecimento dos autores, apenas duas abordagens semelhantes já foram reportadas; na primeira [ZHANG, 2010] apenas o modelo linear válido para baixos sobrepotenciais foi abordado; na segunda [MANDABATTULA; GUPTA, 2012], um supercapacitor simétrico foi modelado, utilizando um modelo macro-homogêneo para a descrição dos eletrodos porosos, contudo não foram apresentados os detalhes da validação do modelo.

Material e métodos

Consideramos um eletrodo metálico plano e homogêneo imerso em uma solução contendo um eletrólito 1:1. Desta forma, utilizamos um modelo 1D, no qual a dimensão de interesse é a distância na direção perpendicular ao eletrodo. O modelo considera a dupla camada elétrica estruturada em duas camadas: uma camada compacta (camada de Stern) de espessura de 0,5 nm e capacitância constante, independente do potencial (ausência de adsorção específica) e uma camada difusa na qual ocorre a separação de cargas na solução. Como a camada compacta tem capacitância constante, ela não foi incluída explicitamente no modelo e apenas utilizada para calcular a densidade de carga superficial sobre o eletrodo. Na camada difusa, o modelo é constituído pelas equações de Nernst-Planck-Poisson. A equação de Poisson é solucionada considerando a densidade espacial de carga dada pelas concentrações dos eletrólitos e a densidade superficial de carga sobre o eletrodo. A equação de Nernst-Planck, assumindo difusão e migração e ignorando a convecção, é usada para calcular as concentrações das espécies do eletrólito. Ambas as equações são acopladas através da interdependência entre potencial e concentração e são solucionadas simultaneamente. O modelo admite uma solução para baixos potenciais aplicados, na qual a carga superficial varia linearmente com o potencial aplicado e uma solução, mais geral, para sobrepotenciais elevados onde a aproximação linear não é válida. Foram realizadas simulações variando o potencial aplicado e a concentração do eletrólito. Adotou-se uma malha ajustada com 232 elementos. Um estudo estacionário típico, conduzido em um PC com processador Intel I7 de 2.7 GHz e 8.0 Gb de memória RAM dura 10 s e ocupa 1,2 GB (1,4 Gb) de memória física (Virtual).

Resultado e discussão

Observa-se na figura 1A que os resultados numéricos são bastante satisfatórios e coincidem com as soluções linear e não linear, para baixos sobrepotenciais, e com a solução não linear, para altos sobrepotenciais. A distribuição de concentração mostrada na figura 1b também é consistente. Quanto mais alto o sobrepotencial maior o acumúlo de carga na solução, de sinal contrário à carga no metal. A visualização da distribuição de concentração (não mensurável) em correspondência ao potencial elétrico na solução é bastante elucidativo para a compreensão do modelo. De particular interesse, é o fato de que, para obter estes resultados, a malha foi refinada utilizando-se um tamanho de elemento para as regiões próximas ao eletrodo e outro tamanho de elemento para as regiões no seio da solução. A malha padrão do COMSOL Multiphysics não forneceu resultados suficientemente próximos à solução analítica. A figura 2 mostra a densidade de carga superficial em função do potencial aplicado, comparando os valores numéricos com a solução analítica linear e não linear. Uma vez mais, os resultados numéricos mostraram-se bastante consistentes, validando o modelo e atestando a adequação do software utilizado. Esta figura é particularmente interessante para mostrar que o modelo linear é válido apenas para potenciais aplicados muito próximos ao potencial de carga zero do metal. Como a capacitância diferencial é obtida pela diferenciação desta curva, fica claro que o cálculo numérico da capacitância também é satisfatório. As simulações variando a concentração de bulk mostram o efeito da compactação da camada difusa com o aumento da concentração.

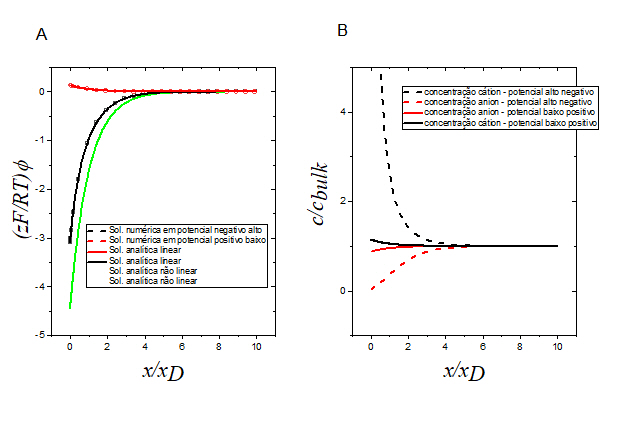
Figura 1A: Distribuição de potencial ao longo da solução. Figura 1B: Concentração correspondente das espécies do eletrólito


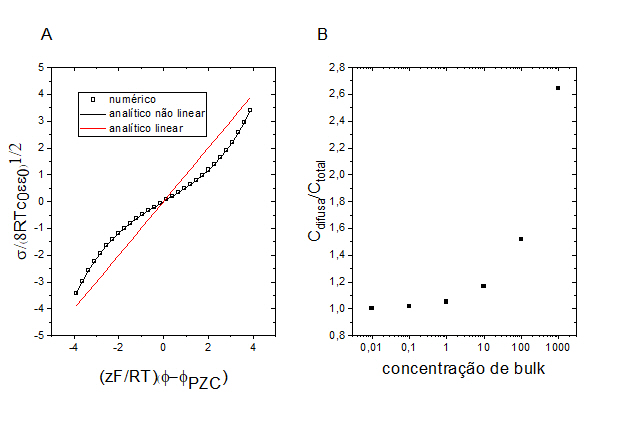
2A)Carga superficial em função do potencial aplicado. 2B) Razão entre capacitância difusa e total em função da concentração do eletrólito.

Conclusões

Os resultados numéricos encontrados para a carga superficial e para a capacitância reproduzem as soluções analíticas lineares, para baixos potenciais e não-lineares, para altos potenciais. Este fato demonstra a validade do modelo e a adequação do software. Os resultados encontrados mostram que a capacitância da dupla camada elétrica varia com o potencial aplicado, com a concentração do eletrólito e com a constante dielétrica. Além disso, esses resultados são facilmente interpretados analisando perfis calculados de concentração e potencial elétrico, não acessíveis experimentalmente.

Agradecimentos

Ao professor Dr. Ernesto Pereira, da Universidade Federal de São Carlos por possibilitar o uso do software COMSOL Multiphysics.

Referências

MANDABATTULLA, G.; GUPTA, S. K. COMSOL Modeling of Supercapacitors. In: COMSOL CONFERENCE 2012. Bangalore. Anais eletrônicos...https://br.comsol.com/papers-presentations/2010

ZHANG, G. Simulating the Electrical Double Layer Capacitance. In: COMSOL CONFERENCE 2010, Boston. Anais eletrônicos...Disponível em https://br.comsol.com/papers-presentations/2012/page/2https://br.comsol.com/papers-presentations/2010