MODELAGEM TERMODINÂMICA DE UM PROCESSO DE CAPTURA DE CO2 UTILIZANDO MONOETALMINA (MEA)

ISBN 978-85-85905-25-5

Área

Físico-Química

Autores

Marinho Guimarães, R. (UNIVERSIDADE FEDERAL DA PARAÍBA) ; Lucena de Morais Pereira, L. (UNIVERSIDADE FEDERAL DA PARAÍBA) ; Oswaldo Alcazar Rojas, L. (UNIVERSIDADE FEDERAL DA PARAÍBA) ; Araújo de Morais Júnior, A. (UNIVERSIDADE FEDERAL DA PARAÍBA)

Resumo

O aquecimento global vem se intensificando a cada dia que passa. Com o aumento gradativo na emissão de gases que incrementam o chamado efeito estufa, responsável pelo aumento na temperatura, desastres e desiquilíbrios ambientais estão cada vez mais evidentes, figurando o dióxido de carbono (CO2) como seu principal agente. Por esse motivo, a implementação de tecnologias voltadas à sua captura é fundamental, sendo a absorção reativa com o uso da solução aquosa de monoetanolamina (MEA) um importante exemplo desses processos. Para que se conheça o limite da operação, deve-se investigar o equilíbrio termodinâmico desse sistema, e, portanto, o trabalhou objetivou investigar o equilíbrio líquido vapor entre MEA e H2O por via modelagem gamma-phi, com os modelos eNRTL e de Soave.

Palavras chaves

eNRTL; Soave; Equilíbrio termodinâmico

Introdução

O aquecimento global é um problema que vem afligindo multidões. De acordo com a Organização das Nações Unidas (ONU), as emissões de poluentes estão aumentando a cada ano, tendo chegado a 52,7 bilhões de toneladas em 2014. O ano de 2015, por exemplo, foi o mais quente desdo início dos registros de temperatura, no século 19. (ASSOCIATED PRESS, 2017; GCP, 2018; NASA, 2018). Dentre as fontes emissoras, as termoelétricas movidas a carvão, a óleo combustível ou a gás natural atuam como principais agentes na emissão de um desses poluentes, o CO2, o qual representa 25% do total de gases emitidos à atmosfera (HOUSE et al., 2009; GCP, 2018). Com o intuito de mitigar essa problemática, vê-se como alternativa a utilização de métodos capazes de capturar esse poluente na exaustão desses gases, e um deles é a absorção, em especial, a reativa com o uso de solventes de aminas aquosas, como a monoetanolamina. Essa alternativa é atraente, por haver um aumento na solubilidade do poluente, o soluto, e uma consequente redução na resistência à transferência de massa (WILCOX, 2012). Um detalhe importante da operação de absorção diz respeito a uma de suas regras heurísticas, mais precisamente a que trata da necessidade de serem utilizados solventes que não sejam voláteis. Para tanto, é necessário que seja investigado o equilíbrio líquido-vapor, para que se possa identificar a tendência de transferência de massa entre as fases (GEANKOPLIS, 1993). Tem- se, portanto, um sistema binário composto pela monoetanolamina, uma amina primária, e a água, que, por se tratarem de compostos com propriedades distintas, provocam uma não-idealidade, e, neste sentido, requere-se uma modelagem que considere esses desvios. A operação em questão é realizada a pressão baixas e moderadas, e, por esse motivo, uma modelagem adequada é a gamma-phi, que utiliza um modelo de atividade para descrever a não- idealidade da fase líquida e uma equação de estado para a vapor (WALAS, 1985). Como projetos futuros a esse envolverão a presença de eletrólitos, usa-se desde já o modelo desenvolvido por CHEN et al. para o coeficiente de atividade em soluções contendo eletrólitos, o electrolyte nonrandon two- liquid, ou eNRTL. Segundo o autor, esse modelo se adequa a todo o intervalo de concentração, o que é um dos adventos do modelo, e, quando na ausência de íons, reduz-se ao modelo de Renon, o nonrandon two-liquid. Outra vantagem diz respeito ao fato de que não se necessita do conhecimento de parâmetros de área e volume para a realização dos cálculos (CHEN, 1982; RENON, 1968). Um revés, contudo, é o fato de ter um caráter mais qualitativo, por motivo da forma como a equação para o coeficiente de atividade ter sido concebido, como é explicado por Hessen, et al. (HESSEN, 2010), contudo seus parâmetros experimentais estão bem disponíveis tanto na literatura, como em softwares de simulação, a exemplo do ASPEN PLUS. A equação de Soave está dentre as equações de estado cúbicas mais populares na indústria química (GMEHLING, 2012). Para o sistema MEA-H2O-CO2, LIU et al. justificam o seu uso como sendo apropriado à simulação do processo de absorção de CO2, por fornecer informações vitais, como a interface de equilíbrio líquido-vapor, a força motriz para a transferência de massa, além de uma boa referência para espécies líquidas reais (LIU, 1999). Por se tratarem de polinômios de terceiro grau, à temperatura constante e a uma dada pressão, existirão sempre três raízes, sejam elas todas reais, ou uma única real e duas complexas conjugadas, o que irá depender dos valores de P e T. Para o caso de três raízes distintas serem encontradas como soluções, aquela que possuir o menor valor corresponderá à fase líquida, a maior à fase vapor e a intermediária não possui sentido físico. Definidos os modelos de não- idealidade, pode-se proceder à resolução do equilíbrio, e existem diversas metodologias para isso, como os algoritmos de orvalho e bolha de temperatura e pressão. A escolha desses métodos deve ser feita mediante as variáveis que são conhecidas. Para os algoritmos de bolha, tem-se conhecimento da composição da fase líquida, ao passo que para os de orvalho sabe-se da composição da fase vapor; a indicação acerca da temperatura e pressão diz respeito a qual dessas propriedades intensivas se busca conhecer, tendo-se a restante em mãos, por consequência. Por exemplo, o algoritmo de bolha-P busca identificar a composição da fase vapor e o valor da pressão do sistema, tendo-se em mãos a composição da fase líquida e o valor da temperatura do sistema (GMEHLING, 2012; SMITH, 2007; WALAS, 1985). Este trabalho, em suma, buscou investigar o equilíbrio líquido-vapor, através da modelagem gamma-phi, por via do algoritmo de bolha de pressão, ou bolha-p.

Material e métodos

Esse trabalho foi desenvolvido em linguagem de programação Matlab. O algoritmo de bolha de pressão foi implementado de forma semelhante ao que é apresentado por Smith et al. (SMITH, 2007). Os parâmetros de interação para o modelo eNRTL foram retirados do arigo de HESSEN, et al. (HESSEN, 2010) e os valores de temperatura crítica, pressão crítica e fator acêntrico, necessários ao cálculo dos coeficientes de fugacidade da monoetanolamina e da água foram obtidos, respectivamente, em publicação de Yaws, et al. (YAWS, 2009) e no livro "The properties of gases and liquids, 5e ed." de Poling et al (POLING, 2000). As constantes para a equação de Antoine e os dados experimentais foram obtidos de Belabbaci et al. (BELABBACI, 2009). Foram construídos os gráficos dos coeficientes de atividades versus fração molar; das curvas de orvalho e bolha com a temperatura fixa; e a curva de equilíbrio para as temperaturas de 293,15 K, 323,15 K, 333,15 K e 363,15 K. Foram gerados 100 pontos para as frações molares para a monoetanolamina e a água dentro do intervalo de zero a um. Os dados do modelo foram comparados ao experimentais por meio do erro quadrático médio (MSE) e da raiz do erro quadrático médio (RMSE).

Resultado e discussão

Os resultados obtidos dizem respeito à parcela do código referente aos componentes moleculares (MEA e H2O). Os dados experimentais foram encontrados na literatura, apartir dos quais pôde-se verificar a validade da parte do modelo referente aos componentes supracitados. De antemão, pode-se verificar que o desvio apresentado é negativo, como pode ser visto nas figuras em anexo, o que é bastante satisfatório, visto que deseja-se que solventes para a absorção não sejam voláteis. Os dados experimentais foram representados sob a forma de cruzes no gráfico da figura 1. Como pode se verificar na tabela 1, o maior erro está na ordem de 10^-2; é visível que o desvio apresentado pelo sistema binário em questão é negativo, como pode ser visto nas figura 1, uma vez que a curva apresenta um perfil abaixo da curva de referência. Conclui-se, portanto, que a regra heurística para a volatilidade do solvente é atendida, visto que o desvio negativo verificado evidencia que a matéria está mais concentrada na fase líquida.

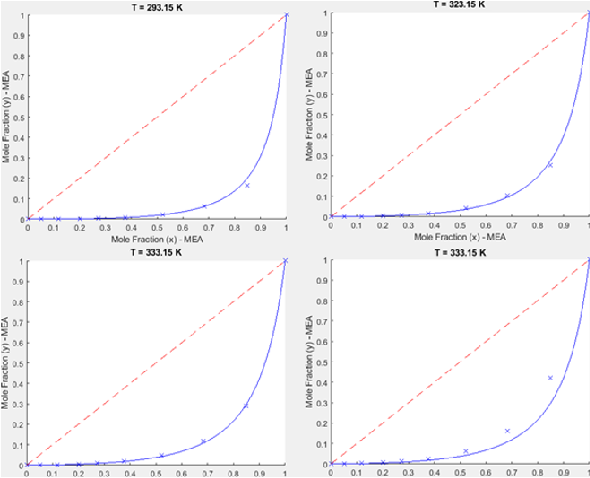
A curva em vermelho corresponde à curva de referência, enquanto a azul à de equilíbrio.


MSE e RMSE para o cálculo da fração molar de monoetanolamina.

Conclusões

Pode-se concluir, diante dos resultados obtidos, que o algoritmo desenvolvido está funcionando de maneira satisfatória. Além disso, também verifica-se que a modelagem empregada está adequada, diante dos erros obtidos. Finalmente, pôde- se chegar à constatação de que o solvente em questão atende ao requisito de não ser volátil, diante do desvio negativo apresentado pela curva de equilíbrio.

Agradecimentos

Agradecimentos à Universidade Federal da Paraíba, juntamente ao orgão de fomento a pesquisa responsável por trazer recursos ao nosso trabalho, a CAPES e a toda a equipe que compõe o Laboratório de Modalagem computacional da UFPB.

Referências

ASSOCIATED PRESS, 2017. By MICHAEL CASEY. Dec. 14, 2017. Disponível em <https://www.apnews.com/084be5202c694d8b93b09c123a2cc8cb.> Último acesso: maio de 2018.
BELABBACI, A. RAZZOUK, A. MOKBEL, I. JOSE, J. NEGADI, L. Isothermal Vapor-Liquid Equilibria of (Monoethanolamine + Water) and (4 Methylmorpholine + Water) Binary Systems at Several Temperatures. Journal of Chemical & Engineering. 2009. P. 2312-2316.
CHEN, C. C; BRITT, H. I.; BOSTON, J. F.; EVANS, L. B. Local Composition Model for Excess Gibbs Energy of Electrolyte Systems. AIChE Journal, p. 588-596, Jul. 1982.
GCP - Global Carbon Project. Índices globais de emissões de CO2: disponível em <http://www.globalcarbonatlas.org/en/CO2-emissions>. Último acesso: agosto de 2018.
GEANKOPLIS, C J. Transport Processes and Unit Operations. . Prentice-Hall. 1993
GMEHLING, J.; KOLBE, B.; KLEIBER, J. R.; RAREY J. Chemical Thermodynamics for Process Simulation. 1. Ed. Weinheim, Wiley-VCH, 2012.
HESSEN, E. T ; WARBERG, T. H. ; SVENDSEN, H. F. The refined e-NRTL model applied to CO2-H2O-alkanolamine systems. Chemical Engineering Science. n. 65, pp. 3638-3648.
HOUSE KZ, HARVEY CF, AZIZ MJ, SCHRAG DP. The energy penalty of postcombustion CO2 capture & storage and its implications for retrofitting the U.S. installed base. Energy Environ Sci 2:193–205, 2009.
LIU,Y; ZHANG, L; WATANASIRI, S. Representing Vapor−Liquid Equilibrium for an Aqueous MEA−CO2 System Using the Electrolyte Nonrandom-Two-Liquid Model. Industrial & Engineering Chemistry Research, p. 2080-2090, Mai. 1999.
NASA - NATIONAL AERONAUTICS AND SPACE ADMINISTRATION. Global Climate change: Vital Signs of the planet. 2018.
POLING, B.E. PRAUSNITZ, J.M. O’CONNEL, J.P. The properties of gases and liquids. 5 ed. McGRAW-HILL. 2000.
RENON, H.; PRAUSNITZ, J. Local Compositions in Thermodynamic Excess Functions for Liquid Mixtures. AlChE Journal, v. 86, v. 14, n. 1, p. 135-144, jan. 1968.
SMITH, J. M.; NESS, H. C. V.; ABBOTT, M. M. Introdução à termodinâmica da engenharia química. 7. Ed. Rio de Janeiro, LTC, 2007.
WALLAS, S.M. Phase equilibria in chemical engineering. Elsevier 688 p. 1985.
WILCOX, J. Carbon Capture. Stanford, CA: Springer, 2012.
YAWS, C. L. NARASIMHAN, P. K. Critical Properties and Acentric Factor. Organic Compounds. Thermophysical Properties of Chemicals and Hydrocarbons. 1-95. 2009.