DETERMINAÇÃO DA MASSA ESPECÍFICA DA POLPA DE MELANCIA ATRAVÉS DE CORRELAÇÕES MATEMÁTICAS

ISBN 978-85-85905-25-5

Área

Alimentos

Autores

Nóbrega, H.L. (IFRN/CA) ; Araújo Filho, M.N. (IFRN/CA) ; Oliveira, R.G.M. (IFRN/CA) ; Melo, J.C.S. (IFRN/CA) ; Costa, C.H.C. (IFRN/CA) ; Badoró, A.D.S. (UFRN)

Resumo

A falta de conhecimento das propriedades termofísicas da polpa de fruta, como a massa específica, acarretará no processamento inadequado da polpa. O objetivo deste trabalho foi determinar experimentalmente a massa específica da polpa de melancia integral em diferentes temperaturas, além de estabelecer uma correlação entre a massa específica da polpa de fruta com a temperatura. Para a determinação da massa específica, foi usado o picnômetro, em triplicata. Os valores experimentalmente da massa específica variaram entre 1033,56 e 1010,36 kg/m³. A massa específica da polpa de melancia diminuiu com o aumento da temperatura. As equações de três e quatro termos apresentaram um bom ajuste, com coeficiente de determinação igual a 0,9990. A energia de ativação encontrada foi igual a 432,06 J/g-mol.

Palavras chaves

Densidade; Polpa de fruta; Equação polinomial

Introdução

A polpa de fruta é um produto com grande aceitação no mercado nacional, pois preserva as características organolépticas, como a cor, sabor e odor, dos frutos (SALGADO et al., 1999, p. 2). A produção de polpas de frutas é uma alternativa para manter a qualidade da fruta e garantir o seu consumo independente da época de safra. Segundo Castro et al. (2015), a fabricação de polpas de frutas congeladas é uma ótima opção nas épocas de safra, possibilitando a comercialização das polpas nos períodos de intermédio entre uma safra e outra. O suco da melancia, por exemplo, contém propriedades atrativas para o consumo, pois é fonte de vitamina A e C, de água e de citrulina, um aminoácido que tem propriedades vasodilatadoras e antioxidantes (PARAENSE et al., 2017, p. 2). De acordo com Andrade Júnior et al. (2007), a melancia é consumida in natura, sendo um alimento depurativo, refrescante e ligeiramente laxante. Segundo Portela (2009), a melancia apresenta versatilidade na forma de consumo, podendo ser consumida in natura, sucos, geleias, drinks, doces, saladas e molhos, como também, a mesma apresenta considerável potencialidade nutricional, uma vez que a polpa se constitui por importantes teores de minerais, como fósforo, potássio, cálcio, ferro, magnésio e de licopeno. No projeto de equipamentos destinados ao processamento de frutas, o conhecimento das propriedades ligadas aos seus padrões de comportamento reológico determina a sua concepção e o dimensionamento de bombas, filtros, tubulações, entre outros (PELEGRINE et al., 2000, p. 128). Dessa forma, a otimização dos processos e o dimensionamento correto dos equipamentos representam um ganho energético e econômico. Para que ocorra a otimização, é necessário o conhecimento das propriedades termofísicas, como por exemplo a massa específica, já que a temperatura e a concentração da polpa de fruta ou suco de fruta pode se dilatar ou contrair dependendo das condições de processamento (PELEGRINE et al., 2000, p. 128; BOLZAN, 2007, p. 227). A massa específica é definida como a massa do produto por unidade de volume, expressa em kg/m3. O cálculo da massa específica é realizado através da Equação 1, que estabelece relação entre massa e volume. ρ = m/v (1) na qual, ρ - Massa específica do produto (kg/m3); v – Volume do picnômetro (m3); m – Massa do produto (kg). A influência da temperatura e concentração na massa específica das polpas de frutas, como por exemplo, a polpa de cajá e umbu (5, 15, 25, 35, 45, 55, 65, 75 e 85°C) e polpa de melancia (10, 20, 30, 40, 50 e 60 °C), respectivamente (SOUZA, 2008, p. 38 – 46; GUEDES et al., 2010, p. 282). O uso dos modelos matemáticos utilizados para prever o comportamento da massa específica da polpa de fruta em relação ao parâmetro temperatura pode ser uma alternativa viável na substituição da análise experimental por ser mais rápida, simples e de menor custo (EGEA et al., 2015, p. 185). Alves et al. (2018), estudando a predição do comportamento da massa específica das polpas de abacaxi e acerola sob diferentes temperaturas através de modelos polinomiais, verificaram que o modelo polinomial de três termos apresentou um bom ajuste, sendo uma alternativa viável para determinar a massa específica das polpas analisadas. Já Egea et al. (2015), ao proporem a modelagem matemática para calcular a massa específica de palmito pupunha, observaram que a modelagem pode ser uma forma eficiente, pois simula condições reais de processamento a fim de prever o seu comportamento. Portanto, o objetivo foi determinar experimentalmente a massa específica da polpa de melancia integral em diferentes temperaturas (10, 20, 30, 40 e 50°C), além de estabelecer uma correlação entre a massa específica da polpa de frutas com a temperatura, utilizando modelos matemático polinomiais com dois, três e quatro termos.

Material e métodos

As frutas foram adquiridas no comércio da cidade de Caicó/RN. Posteriormente, foram lavadas em água corrente e depois imersas em uma solução de hipoclorito de sódio a 50 ppm, durante 15 minutos; em seguida, foram enxaguados e despolpados utilizando um multiprocessador. Logo após, as polpas foram envasadas e armazenadas em um refrigerador. As análises da massa específica das polpas de frutas foram realizadas em triplicata, nas temperaturas de 10, 20, 30, 40 e 50°C e na concentração de 8,2 °Brix. Foram usados picnômetros previamente calibrados. Os cálculos da massa específicas foram de acordo com a equação 1 descrita abaixo. ρ = m/v (1) onde: ρ – é massa especifica (kg/m³); m- é massa do produto (kg); v- é volume do picnômetro (m³). As temperaturas das amostras foram controladas através do banho termostato e por meio dos termômetros. Quanto a modelagem matemática da massa específica da polpa, foram utilizados os modelos polinomiais, linear (2), de três termos (3) e com quatro termos (4) descritos abaixo. ρ =a+bT (2) ρ =a+bT+cT² (3) ρ =a+bT+cT2+dT3 (4) na qual, T – Temperatura (ºC); a, b, c e d – constantes. Para a obtenção dos valores da energia de ativação para a massa específica Ea foi empregado o método proposto por Tsen e King (2002), na qual a Equação (2) é escrita na forma de: ρ=ρoxExp(Ea/RT) (2) Onde: ρ0 é massa específica (kg/m3); Ea: energia de ativação (J/g-mol); R: constante universal dos gases (8,3144 J/g-mol K); T: temperatura absoluta (K). O ajuste dos modelos foi realizado pelo método Quasi-Newton por meio de análises de regressão não linear. O grau de ajuste de cada modelo foi considerado pela magnitude do coeficiente de determinação (R²). Foram feitas regressões lineares dos dados da massa especifica para obtenção das equações que representa essa grandeza, utilizando o programa STATISTICA.

Resultado e discussão

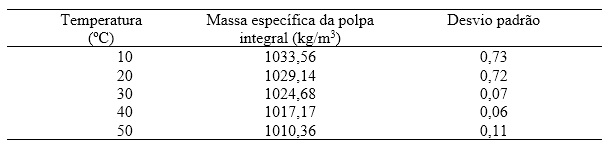
Na Tabela 1 têm-se os valores experimentais da massa específica da polpa de melancia nas temperaturas de 10 a 50 ºC, e seus respectivos desvios padrão. O valor da massa específica da polpa de melancia variou de 1033,56 a 1010,36 kg/m3. Guedes et al. (2010), estudando o comportamento da massa específica da polpa de melancia observaram que a massa específica da polpa de melancia variou de 1035,0 a 1015,2 kg/m3. Nota-se ainda que a massa específica da polpa de melancia diminuiu com o aumento da temperatura. Oliveira et al. (2018) observaram durante estudos sobre a polpa de abacaxi que a massa específica apresentou tendência a diminuir quando houve aumento da temperatura, em seu experimento. Segundo Diniz et al. (2014), os valores de massa específica diminuem com o aumento da temperatura provavelmente devido à expansão volumétrica do fluido causada pela redução da ligação da força intermolecular. Na Tabela 2 encontram-se as equações utilizadas para descrever o efeito da temperatura sobre a variação da massa específica da polpa de melancia e seus respectivos coeficientes de determinação. Observa-se que as três equações podem ser utilizadas para predizer a massa especificas da polpa de melancia, embora os modelos polinomiais com três e quatro termos apresentaram os maiores coeficientes de determinação, sendo aqueles que melhor se ajustaram aos dados experimentais. Alves et al. (2017), estudando três modelos representados por equações polinomiais propostas para o cálculo da massa específica da polpa da goiaba em função da temperatura, perceberam que o modelo que melhor se ajustou aos dados experimentais, considerando o maior coeficiente de determinação, foi o modelo polinomial com quatro termos, com R2 =0,9979. Lima et al. (2002), estudando equações do tipo linear, quadrática e polinomial de quatro termos para representar o comportamento da massa específica da polpa de cupuaçu, concluíram que a equação polinomial de quatro termos apresentou melhor ajuste com coeficientes de determinação (R2) superiores a 0,99. Quanto ao valor da energia de ativação do modelo de Arrhenius (Tabela 2), calculado a partir da relação da massa específica com a variação da temperatura para a polpa de melancia, foi igual a 432,06 J/g-mol para a energia de ativação. Tsen e King (2002), obtiveram valores de energia de ativação variando de 748,36 a 1137,36 J/g-mol para o purê de banana, com as concentrações de sólidos solúveis variando de 10 a 80 ºBrix e temperaturas de 5 a 80 ºC.

ρ - Massa especifica (kg.m-3); T – Temperatura (ºC); R2– coeficiente de determinação; Ea – Energia de ativação.

Conclusões

A massa específica da polpa de melancia com 8,2°Brix diminuiu com o aumento da temperatura. O modelo matemático polinomial que melhor prediz a massa específica da polpa de melancia foram o de três e quatro termos, embora o modelo de dois termos também pode ser utilizado. O valor da energia de ativação determinada para a polpa de melancia foi igual a 432,06 J/g-mol, verificando a sensibilidade da polpa de melancia com a variação da temperatura.

Agradecimentos

Ao IFRN/CA pelo incentivo à pesquisa.

Referências

ANDRADE JÚNIOR, A. S.; RODRIGUES, B. H. N.; SOBRINHHO, C. A.; BASTOS, E. A.; MELO, F. B.; CARDOSO, J. M.; SILVA, P. H. S; DUARTE, R. L. R. A cultura da melancia/Embrapa Meio-Norte – 2ª ed. rev. amp.– Brasília, DF: Embrapa Informação Tecnológica, 2007. 85 p. il. (Coleção Plantar, 57).
ALVES, M. N. M.; SILVA, D. A.; MELO, J. C. S.; COSTA, C. H. C.; Badaró, A. D. S. Avaliação de modelos polinomiais para estimar a massa específica da polpa de goiaba. In: CONGRESSO BRASILEIRO DE QUÍMICA, 2017, Gramado. 57º CONGRESSO BRASILEIRO DE QUÍMICA, 2017
ALVES, M. N. M.; SANTOS, D.A.; MELO, J. C. S.; COSTA, C. H. C.; BADARÓ, A. D. S.; FEITOSA, R. M. Predição do comportamento da massa específica das polpas de abacaxi e acerola sob diferentes temperaturas. Revista Agropecuária Técnica, v. 39, n. 2, p. 158-163, 2018.
BOLZAN, T. G.; SOUZA, D. Estudo do comportamento da massa especifica de suco de laranja em função da temperatura e da concentração. XIX Salão de iniciação científica, Livro de resumos. Porto Alegre: UFRGS, 2007. Disponível em: < http://www.lume. ufrgs.br/bitstream/handle/10183/57965/Resumo_200701575.pdf?sequence=1 > Acesso em: 02 Sep. 2018.
CASTRO, T.M.N.; ZAMBONI, P.V.; DOVADONI, S.; CUNHA NETO, A.; RODRIGUES, L.J. Parâmetros de qualidade de polpas de frutas congeladas. Revista Inst Adolfo Lutz, v.74, n.4, p.426-36, 2015
DINIZ, R. S.; COIMBRA, J. S.R.; MARTINS, M. A.; SANTOS, M. O.; DINIZ, M. D. M. S.; SANTOS, E. S.; SANTÁNNA, D. D.; ROCHA, R. A.; OLIVEIRA, E. B. Physical Properties of Red Guava (Psidium guajava L.) Pulp as Affected by Soluble Solids Content and Temperature. International Journal of Food Engineering, v.10, n.3, p. 437–445, 2014.
GUEDES, D. B.; RAMOS, A. M.; DINIZ, M. D. M. S. Efeito da temperatura e da concentração nas propriedades físicas da polpa de melancia. Brazilian Journal of Food Technology, Campinas, v. 13, n. 4, p. 279-285, 2010.
EGEA, M. B.; REIS, M. H. M.; DANESI, E. D. G. Aplicação de modelos matemáticos preditivos para o cálculo das propriedades termofísicas do palmito pupunha. Revista Brasileira de Produtos Agroindustriais, v.17, n.2, p.179-187, 2015.
LIMA, Í. J. E.; QUEIROZ, A. J. M.; FIGUEIRÊDO, R. M. F. Propriedades termofísicas da polpa de umbu. Revista Brasileira de Produtos Agroindustriais, Especial, n.1, p.31-42, 2003.
MATTA, V. M.; FREIRE JUNIOR, M.; CABRAL, L. M. C.; FURTADO, A. A. L. Polpa de fruta congelada. Brasília,DF: Embrapa Informação Tecnológica, 2005. 35 p. (Embrapa Informação Tecnológica. Agroindústria Familiar).
OLIVEIRA, R. G. M.; SOUZA, W. M.; MELO, J. C. S.; COSTA, C. H. C.; BADARÓ, A. D. S.; "PREDIÇÃO DA MASSA ESPECÍFICA DA POLPA DE ABACAXI ATRAVÉS DE EQUAÇÕES MATEMÁTICAS", p. 2853-2856 . In: . São Paulo: Blucher, 2018.
PARAENSE, M. O.; AULER, P. E.; FIGUEIREDO, K. C. S.; Clarificação de suco de melancia através de microfiltração com membrana de acetato de celulose. The Journal of Engineering And Exact Sciences, [s.l.], v. 3, n. 3, p.584-594, 9 maio 2017. Universidade Federal de Vicosa..
PELEGRINE, D. H.; VIDAL, J. R. M. B.; GASPARETTO, C. A. Estudo da viscosidade aparente das polpas de manga (Keitt) e abacaxi (Pérola). Ciência e Tecnologia de Alimentos, Campinas , v. 20, n. 1, p. 128-131, Apr. 2000.
PORTELA, Julianne Viana Freire. Estudo dos aspectos tecnológicos e de qualidade envolvidos no aproveitamento da casca e da polpa da melancia. 2009. 130 f. Dissertação (Mestrado) - Curso de Ciência e Tecnologia de Alimentos, Centro de Tecnologia, Universidade Federal da Paraíba, João Pessoa - Pb, 2009.
SALGADO, S. M.; GUERRA, N. B.; MELO FILHO, A. B. Polpa de fruta congelada: efeito do processamento sobre o conteúdo de fibra alimentar. Revista de Nutrição, Campinas, v. 3, n. 12, p.303-308, dez. 1999.
SOUZA, Michelle Andrade. Determinação das propriedades termofísicas de polpas de frutas tropicais: Jaca (Artocarpus Heterophilus Lamk.) e Umbu (Spondias Tuberosa Arr. Cam.). 2008. 65 f. Dissertação (Mestrado) - Curso de Engenharia de Processo de Alimentos, Universidade Estadual do Sudoeste da Bahia, Itapetinga, 2008.
TSEN, J. H.; KING, V. A. E. Density of banana puree as a function of soluble solids concentration and temperature. Journal of Food Engineering, v.55, n.4, p.305-308, 2002.