Realizado no Rio de Janeiro/RJ, de 14 a 18 de Outubro de 2013.
ISBN: 978-85-85905-06-4
ÁREA: Físico-Química
TÍTULO: INCLUSÃO DO FATOR ESTÉRICO NUM MODELO ESTOCÁSTICO BASEADO NO MÉTODO DE MONTE CARLO: APLICAÇÃO NO ESTUDO DE REAÇÕES QUÍMICAS IRREVERSÍVEIS
AUTORES: Araújo, D.M. (UESB) ; Oliveira, F.A. (UESB) ; Cardoso, L.A.M. (UESB) ; Farias, R.R. (UESB) ; Oliveira-neto, N.M. (UESB) ; Couto, A.L. (UESB) ; Nascimento, F.P. (UESB) ; Nascimento Junior, B.B. (UESB)
RESUMO: Neste trabalho, realizamos simulações computacionais de reações químicas
homogêneas, elementares e irreversíveis utilizando o Método de Monte Carlo
(MMC), o qual consiste na probabilidade da reação direta ocorrer. Essa
probabilidade de transição é baseada na energia de ativação da reação direta
(Ea), da energia térmica média das moléculas (kBT); também, incluímos um novo
parâmetro (ps) que imita o fator estérico nas reações. Os resultados simulados
mostram que a inclusão deste fator estérico, como proposto neste trabalho,
simula qualitativa e quantitativamente os resultados da literatura, mostrando
ser uma forma simples e efetiva de se incluir, na probabilidade de transição, o
fator geométrico inerente nas reações químicas.
PALAVRAS CHAVES: Fator Estérico; Monte Carlo; Simulação Computacional
INTRODUÇÃO: Os estudos de reações químicas são realizados em laboratórios e os
resultados experimentais são, em geral e quando possível, confrontados com a
teoria ou vice-versa. Porém, para realização deste trabalho utilizaremos um
laboratório computacional no qual realizaremos simulações computacionais para
estudar reações de primeira ordem homogêneas, via Método Monte Carlo. A
abordagem computacional tem como vantagem a obtenção de resultados que nem
sempre são obtidos em laboratórios usuais devido a fatores de regimes
extrapolados como temperaturas e pressões (FARIAS et. al., 2013). Utilizando um
modelo matemático já proposto na literatura (FARIAS et. al., 2013) para o estudo
de reações químicas do tipo A → B , incluímos um parâmetro pré-exponencial ps
com o intuito de simular os fatores geométricos (fator estérico) inerentes em
reações químicas. Este fator estérico ps, também chamado “fator de
probabilidade”, é a fração de colisões nas quais as moléculas estão
favoravelmente orientadas à reação (o qual pode ser determinado
experimentalmente). O mesmo possui valor entre zero e um, sendo que para a
grande maioria das reações assume um valor muito baixo (CIRINO et. al., 2010).
A constante de velocidade k de uma reação química segue uma lei de Arrenhius da
forma k=A exp(Ea/RT), onde k é a constante de velocidade, A é o fator pré-
exponencial, Ea a energia de ativação por mol, R constante universal dos gases
ideais e T temperatura absoluta. O fator pré-exponencial A, depende, dentre
outros fatores, da orientação das moléculas durante as colisões. Com
isso,influencia diretamente na velocidade das reações químicas. É exatamente
esta dependência qualitativa e quantitativa que objetivamos incluir num modelo
matemático estocástico proposto na literatura (FARIAS et. al., 2013).
MATERIAL E MÉTODOS: Definimos a probabilidade de transição, para a reação direta, PAB, via
atualização de Metropolis, como segue:
PAB=psexp(-βEa)
onde β = (kBT)-1, kB é a constante de Boltzmann, T é a temperatura absoluta, Ea
é a energia de ativação da reação direta, e ps é um parâmetro para imitar o
fator estérico das reações.
Para obtenção dos resultados, utilizamos o modelo de Urna de Ehrenfest. (FARIAS
et. al., 2011) Inicialmente indexamos todas as moléculas por um índice i = 1,
...,N. Após, seguimos o seguinte passo:
(I) Selecionamos aleatoriamente uma molécula do tipo A; um número aleatório
uniforme z ∈ [0, 1] é gerado e comparado com PAB; se z ≤ PAB a reação ocorre e
A torna-se B. Se não, a molécula permanece em sua forma original e o passo
termina.
Executando o passo acima, para N (número de moléculas) vezes, definimos o passo
de Monte Carlo.
RESULTADOS E DISCUSSÃO: Neste trabalho, foi simulado uma reação A→B. Na Figura 1 exibimos a dinâmica das
frações em mols de A e B sem a influência do fator estérico, i.e. ps=1. Como
podemos observar o reagente A é completamente consumido, enquanto que temos a
formação do produto B. No gráfico interno da Figura 1, observa-se, em escala
logarítmica, que XA em função do passo de MC, assume uma reta evidenciando o
comportamento de uma reação de primeira ordem. Para este caso, ps=1, realizando
simulações para diferentes
temperaturas θ, é possível chegar na lei de Arrhenius, com A ≈1 (FARIAS et. al.,
2013). Na figura 2, exibimos a evolução temporal da fração em mols XA, para
diferentes valores de ps, no intervalo 0<ps<1. Nesta figura, podemos observar
que à medida que ps diminui, XA decai mais lentamente, corroborando
qualitativamente com o fato de que quanto menor o fator estérico, menor a
velocidade da reação química.
Quando, por exemplo, ps=0,25, onde apenas 25% das colisões energeticamente
favoráveis terão orientação necessária para a reação ocorrer. Quando ps assume
valor igual a 1, significa que todo choque entre moléculas é orientado de forma
favorável para que ocorra a transformação.
Figura 1
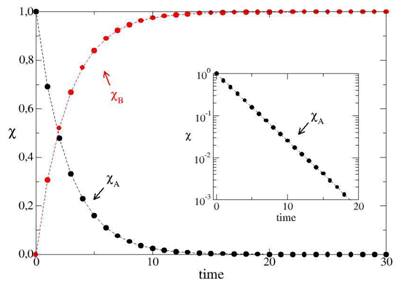
Evolução de XA e do XB em função do passo de MC. A inserção mostra a representação gráfica da fração XA na escala logarítmica.
Figura 2
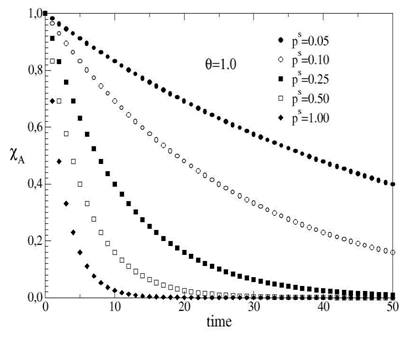
Evolução de XA em função do passo de Monte Carlo (MC) para uma reação do tipo A→B e para cinco valores de fator estérico ps diferentes.
CONCLUSÕES: A partir dos resultados foi possível observar que nossas simulações conseguem
reproduzir satisfatoriamente os resultados da literatura. Também, a maneira como
foi incluído o fator estérico na probabilidade de transição, tal modelo matemático
pode simular o fator geométrico das colisões entre as moléculas reagentes,
implicando numa alteração nas velocidades da reação tal qual aquela observada na
literatura.
AGRADECIMENTOS: UESB, CNPq, CAPES.
REFERÊNCIAS BIBLIOGRÁFICA: 1 FARIAS, R. R., CARDOSO, L. A. M., and OLIVEIRA-NETO, N. M., A Simple Model to Access Equilibrium Constants of Reactions. Exatas Online, 2, 7 (2011).
2 FARIAS, R. R., CARDOSO, L. A. M., OLIVEIRA-NETO, N. M., NASCIMENTO-JUNIOR, B. B. J. Estudo das Reações Químicas Homogêneas Via Método de Monte Carlo. Quim. Nova, Vol. 36, No. 5, 729-733, 2013.
3 CIRINO, M. M., SOUZA, A. R. de, O tratamento probabilístico da teoria cinética de colisões em livros de Química brasileiros para o ensino médio. Revista Electrónica de Enseñanza de las Ciencias Vol. 9, No 1, 125-144, 2010.
