Realizado no Rio de Janeiro/RJ, de 14 a 18 de Outubro de 2013.
ISBN: 978-85-85905-06-4
ÁREA: Físico-Química
TÍTULO: A VISCOSIDADE DE HIDROCARBONETOS EM ALTAS PRESSÕES SEGUNDO A EQUAÇÃO DE ANDRADE-GUZMÁN.
AUTORES: Pires, K.P.N. (UFF) ; Lamego, L.S.R. (UFF) ; Martins, R.J. (UFF)
RESUMO: Neste trabalho pretendeu-se investigar a aplicabilidade da equação de Andrade-
Guzmán na descrição da viscosidade de líquidos em pressões superiores à pressão
atmosférica. Para tanto, o comportamento viscoso de diversos hidrocarbonetos (C1-
C12) foi analisado com base nessa equação em diferentes intervalos de temperatura
e pressão. Buscou-se, também, analisar a dependência dos parâmetros das equações
de correlação obtidas com o número de carbonos dos compostos estudados.
PALAVRAS CHAVES: viscosidade; pressão; temperatura
INTRODUÇÃO: A viscosidade de fluidos mostra-se como uma propriedade de grande importância
para o desenvolvimento e aprimoramento dos diversos processos químicos nas
indústrias de um modo geral.
Diversos estudos têm sido efetuados de modo a obter equações que possam
descrever a viscosidade em amplas faixas de temperatura e pressão, pois existe a
dificuldade de obtenção de dados experimentais em todos os estados relevantes no
âmbito tecnológico. Neste estudo buscou-se testar a aplicabilidade da equação de
Andrade-Guzmán em situações de pressão e temperatura diferentes da aplicação
usual. O tratamento matemático utilizado indicou uma dependência parabólica dos
parâmetros da equação com a pressão. Foi observada uma tendência do
comportamento desses parâmetros quando correlacionados com o número de carbonos
dos compostos estudados.
MATERIAL E MÉTODOS: Dados experimentais de viscosidade do metano, etano, propano, n-butano, n-
pentano, n-hexano, n-heptano, n-octano, n-nonano, n-decano, cis-decalina, n-
undecano, n-dodecano, foram correlacionados, através do Método dos Mínimos
Quadrados Linear, utilizando-se a equação de Andrade-Guzmán (η = A exp(B/T))
linearizada para conjuntos de dados isobáricos. Nessa etapa, foram obtidos os
parâmetros característicos da equação de Andrade-Guzmán. Para cada composto
investigado, o efeito da pressão sobre os parâmetros A e B dessa equação foi
analisado. Para obter uma relação capaz de descrever a dependência dos
parâmetros A e B com a pressão, o Método dos Mínimos Quadrados Linear foi
novamente utilizado e, verificou-se que, ambos satisfazem equações de 2º grau: A
= A0 + A1.p + A2.p² e B = B0 + B1.p + B2.p². Em seguida, buscou-se obter uma
relação entre os novos parâmetros (independentes da pressão) com o número de
carbonos dos compostos estudados. O programa utilizado para fazer as correlações
foi escrito em Pascal, em ambiente Lazarus, e o computador usado foi um pc com
uma cpu AMD de 2,2GHz com sistema Linux – Ubuntu.
RESULTADOS E DISCUSSÃO: Para cada composto investigado foram determinados os parâmetros característicos
da equação de Andrade-Guzmán, A e B, através da minimização de dados
experimentais de viscosidade encontrados na literatu-ra, o que nos permitiu
observar a dependência dos parâmetros da equação com a pressão exercida sobre o
sistema. Apesar de, originalmente ter sido proposta para descrever o efeito da
temperatura sobre a viscosidade de líquidos puros à pressão atmosférica, nosso
estudo mostrou que a equação de Andrade-Guzmán pode ser utilizada em pressões
elevadas. Na figura 1 estão representados os valores experimentais (símbolos) e
os calculados com a equação de Andrade-Guzmán (linhas contínuas) de viscosidade
do n-pentano em diferentes temperaturas e no intervalo de pressão de 4 a 31 MPa.
Desvios relativos médios percentuais da ordem de 3 % foram observados para todos
os compostos investigados, o que nos permite concluir que a equação de Andrade-
Guzmán é adequada para descrever tanto o efeito da temperatura quanto o da
pressão sobre a viscosidade dos líquidos investigados, com as modificações
propostas neste trabalho. Analisando-se o comportamento dos parâmetros A e B com
a pressão, verificou-se que esses parâmetros satisfazem equações de 2º grau,
cujos coeficientes de ordem zero, um e dois, mostram um perfil de dependência
com o número de carbonos presentes na cadeia. Foram observados diferentes perfis
de comportamento para a dependência dos parâmetros A0, A1, A2 e B0, B1, B2 com o
número de carbonos dos componentes estudados. Na figura 2 estão locados os
valores do parâmetro B0 calculado para os diversos conjuntos de dados
experimentais utilizados neste trabalho, onde cada ponto representa um diferente
conjunto de dados isobáricos.
Figura 1
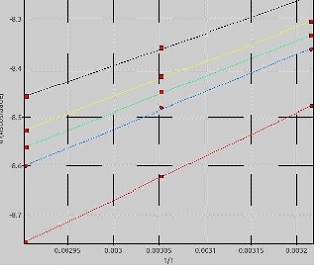
Viscosidade do n-pentano em diferentes temperaturas
e pressões no intervalo de 4 a 31 MPa.
Figura 2
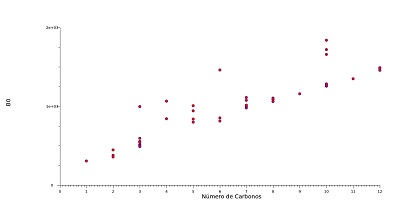
Comportamento do Parâmetro B0 com o Número de
Carbonos Presentes na Molécula.
CONCLUSÕES: Verificou-se que a equação de Andrade-Guzmán pode ser aplicada no cálculo da
viscosidade de líquidos em pressões diferentes da atmosférica com bons resultados.
No caso dos hidrocarbonetos investigados, observou-se uma dependência quadrática
dos parâmetros característicos da equação de Andrade-Guzmán com a pressão e que os
parâmetros das equações de segundo grau estão relacionados ao tamanho da cadeia
carbônica.
AGRADECIMENTOS: Os autores agradem à FAPERJ e à PROPPI/UFF pelo apoio financeiro.
REFERÊNCIAS BIBLIOGRÁFICA: 1) Huang, E. T. S; Swift, G. W.; Kurata, F.; A.I.Ch.E. Journal 1966, 932
2) Friend, D. G.; Ingham, H.; Ely, J. F.; J. Phys. Chem. Ref. Data 1991, 275
3) Starling, K. E.; Eakin, B. E.; Ellington, R. T.; A.I.Ch.E. Journal 1960,438
4) Holland, P. M.; Hanley, H. J.M.; Gubbins, K. E; Haile, J.M.; J. Phys. Chem. Ref. Data 1979, 559.
5) Lee, A. L.; Ellington, R. T.; J. Chem. Eng. Data 1965, 101.
6) Lee, A. L.; Ellington, R. T.; J. Chem. Eng. Data 1965, 346
7) Brazier, D. W.; Freeman, G. R.; Can. J. Chem. 1969, 893.
8) Barrufet, M. A.; Hall, K. R.; Baltazar, A. E.; Silva, G. A. I.; J. Chem. Eng. Data 1999, 1310.
9) Ducoulombier, D.; Zhou, H.; Boned, C.; Peyrelasse, J.; Saint-Guirons, H.; Xans, P.; J. Phys. Chem. 1986, 1692.
10) Hogenboom, D. L.; Webb, W.; Dixon, J. A.; J. Chem. Phys. 1967, 2586.
11) Kuss, E.; Pollmann, P.; Z. Phys. Chem. Neue Folge 1969, 205.
12) Baylaucq, A.; Boned, C.; Daugé, P.;. Lagourette, B; Int. J. Thermophys. 1997, 3.
13) Friend, D. G.; Ingham, H.; Ely, J. F.; J. Phys. Chem. Ref. Data 1991, 275.
14) Mikkelsen, C. K. Z.; Watson, G.; Baylaucq, A.; Galliéro, G.; Boned, C.; Fluid Phase Equilib. 2006, 6.
15) Rastorguyev, Y. L.; Keramidi, A. S.; Fluid Mech. 1974, 1156.
16) Scalabrin, G.; Marchi, P.; Span, R.; J. Phys. Chem. Ref. Data 2006, 1415.
17) Hubbard, R. M.; Brown, G. G.; Ind. Eng. Chem. 1943, 1276.
