Realizado no Rio de Janeiro/RJ, de 14 a 18 de Outubro de 2013.
ISBN: 978-85-85905-06-4
ÁREA: Físico-Química
TÍTULO: MODELAGEM DA VISCOSIDADE DE LÍQUIDOS ATRAVÉS DA EQUAÇÃO DE VISWANATH-NATARAJAN
AUTORES: Savignon, L.T. (UFF) ; Martins, R.J. (UFF) ; Lamego, L.S.R. (UFF)
RESUMO: Neste trabalho, propõem-se encontrar uma relação entre os parâmetros da equação de
viscosidade de Viswanath-Natarajan e o número de carbonos dos diferentes compostos
de séries homólogas. Os líquidos investigados foram n-alcanos (C4 a C19), álcoois
primários (C1 a C11), alquil aminas primárias (C3 a C8) e monoaldeídos (C2 a C7).
A partir desta relação pretende-se estimar a viscosidade destes compostos
utilizando-se o conceito de contribuição de grupos.
PALAVRAS CHAVES: viscosidade; séries homólogas; temperatura
INTRODUÇÃO: Existem várias equações empíricas que descrevem satisfatoriamente o efeito da
temperatura sobre a viscosidade de líquidos. Uma delas é a equação de Viswanath-
Natarajan, η=BTA, onde η é a viscosidade dinâmica, T a temperatura em Kelvin, A
e B são parâmetros característicos do líquido investigado. Neste estudo, o
efeito do tamanho da cadeia carbônica sobre os parâmetros (A e B) da equação de
Viswanath-Natarajan foi avaliado em diferentes séries homologas. Para isso, o
comportamento viscoso, de cada composto das séries homólogas constituídas por
hidrocarbonetos lineares, álcoois primários, alquil aminas primárias e
monoaldeídos, foi investigado em diferentes temperaturas. Manipulações
algébricas e o método de mínimos quadrados foram utilizados para se obter uma
relação entre estes parâmetros e o número de carbonos.
MATERIAL E MÉTODOS: Dados experimentais de viscosidade dinâmica dos líquidos investigados (n-alcanos
(C4 a C19), álcoois primários (C1 a C11), alquil aminas primárias (C3 a C8) e
monoaldeídos (C2 a C7) em diferentes temperaturas, disponíveis na literatura,
foram utilizados para determinar os parâmetros da equação de Viswanath-Natarajan.
Esta equação foi linearizada e o método dos mínimos quadrados linear foi utilizado
na obtenção dos valores de lnB e A. Estudou-se a dependência desses parâmetros com
o número de carbonos para cada série homóloga. O programa utilizado para fazer as
correlações foi o Origin 3.0, em ambiente Windows XP, e o computador usado foi um
pc com uma cpu AMD de 2,2GHz.
RESULTADOS E DISCUSSÃO: A equação descreveu a viscosidade de todos os compostos selecionados, como
ilustra a figura 1 para o n-octadecano, em todo o intervalo de temperaturas
investigadas. Os conjuntos de dados apresentaram um desvio relativo médio global
de 2%. Para cada composto determinaram-se os parâmetros da equação, A e B,
através da minimização de dados experimentais de viscosidade, encontrados na
literatura. Uma vez determinados estes parâmetros, a viscosidade foi calculada e
o desvio relativo absoluto médio (DRAM) percentual foi obtido. DRAM (%) =
(100/N)∑[(|ηExp-ηCal|)/ηExp] onde os índices
Exp e Cal referem-se aos dados experimentais e calculados. Utilizou-se o método
dos mínimos quadrados linear para estudar a dependência entre os parâmetros e o
número de carbonos, quando se observou um comportamento linear em ambos os
casos, onde os coeficientes de correlação se encontram na faixa de 0,78906 até
0,94498. Obtendo-se as seguintes equações: A=A0+A1*NC e lnB = B0+B1*NC; sendo
NC, o número de carbonos, e B0, A0, B1, A1, parâmetros característicos das
séries homólogas. Observou-se que o valor do parâmetro A é decrescente com o
número de carbonos, diferentemente do apresentado pelo parâmetro lnB, em todas
as séries homologas estudadas. Assim, a equação de viscosidade de Viswanath-
Natarajan pode ser alterada para η=(exp(B0+B1×NC))× T^(A0+A1×NC). Porém com
coeficientes de correlação não satisfatórios. Com o intuito de melhorar a
precisão dos cálculos, estudou-se a dependência de lnB/A com o número de
carbonos, que apresenta um perfil linear, com coeficientes de correlação
próximos de um, quando descrita como NC/(a+b×NC) + c. A figura 2 mostra os
gráficos referentes às séries estudadas. A inclinação e os interceptos de cada
reta são característicos da série.
Figura 1

Gráfico linearizado do octadecano para valores
experimentais (□) e teóricos (●) de viscosidade.
Figura 2
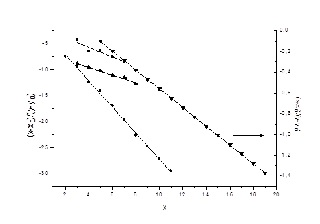
N-alcanos(▼)(eixo direito), álcoois primários(●),
aquil aminas primarias (▲) e monoaldeídos(■); sendo
x o número de número de carbonos,e y, lnB/A.
CONCLUSÕES: Foi observada que a equação de viscosidade de Viswanath-Natarajan é excelente para
descrever o comportamento da viscosidade frente à variação de temperatura para as
séries estudadas. E que há uma relação entre os parâmetros da equação e o número
de carbonos presentes nos compostos estudados. Logo, uma estratégia de
contribuição de grupos pode ser utilizada para a previsão desses parâmetros. Esse
estudo ainda se encontra em desenvolvimento.
AGRADECIMENTOS: Os autores agradecem a CAPES, FAPERJ e PROPPI/UFF pelo apoio financeiro.
REFERÊNCIAS BIBLIOGRÁFICA: VISWANATH, D. S.; NATARAJAN, G. 1989. Data Book on the Viscosity of Liquids. Hemisphere Publishing Corporation.
VISWANATH, D. S.; GHOSH, T. K.; PRASAD, D. H. L.; DUTT, N. V. K.; RANI, K. Y. 2007. Viscosity of Liquids Theory, Estimation, Experiment, and Data. Springer.
YAWS, C. L. 1994. Handbook of Viscosity v.2. Organic compounds C5 to C7. Gulf Publishing Company.
WENG, W.L. 1999. Viscosities and densities for binary mixtures of anisole with 1-butanol, 1-pentanol, 1-hexanol, and 1-octanol. Journal of Chemical and Engineering Data.
OSWAL, S.L 2001. Studies of viscosities and excess molar volume of binary mixtures 3.1-Alkanol+ di-n-propylamine, and+ di-n-butylamine mixtures at 303,15 and 313,15K. Fluid Phase Equilibria.
AL-JIMAZ, A.S.; AL-KANDARY, J.A.; ABDUL-LATIF, A.M. 2004. Densities and viscosities for binary mixtures of phenetole with 1-pentanol, 1-hexanol, 1-heptanol, 1-octanol, 1-decanol at different temperatures. Fluid Phase Equilibria.
