ÁREA: Ensino de Química
TÍTULO: ESTIMATIVA DE PARÂMETROS DE ISOTERMAS DE EQUILÍBRIO DE ADSORÇÃO POR ANÁLISE DE REGRESSÃO NÃO-LINEAR
AUTORES: Lima, A.C.A. (UFC) ; Vidal, C.B. (UFC) ; Santos, G.C. (UECE) ; Raulino, G.S.C. (UFC) ; Nascimento, R.F. (UFC)
RESUMO: A linearização de dados implica em alteração de erros estruturais. Como alternativa, otimizações não lineares podem ser utilizadas para estimação de parâmetros. Neste estudo foram utilizados o Origin e Excel para estimar os parâmetros de quatro modelos de isoterma de adsorção (Langmuir, Freundlich, Redlich-Peterson e Temkin) e cinco funções erros (soma do quadrado dos erros, função erro fracionário hibrido, desvio padrão percentual de Marquardt, erro Relativo médio e soma do erro absoluto) foram examinados. Não houve diferença significativa entre os programas, porém o Excel possui a vantagem da configuração de várias funções erros em busca do mínimo global. Para a isoterma de equilíbrio de Langmuir, a função erro fracionário hibrido foi a que obteve melhor estimativa dos parâmetros.
PALAVRAS CHAVES: REGRESSÃO LINEAR; FUNÇÃO ERRO; ISOTERMAS DE ADSORÇÃO
INTRODUÇÃO: A análise de regressão é uma ferramenta estatística que permite encontrar relação entre a variável dependente, y, e a variável x (SEBER e WILD, 2003). Os modelos de regressão podem ser classificados como lineares e não lineares. Os modelos não lineares, por sua vez, são classificados como intrinsecamente linear, quando podem ser linearizados por reparametrização ou transformação, e intrinsecamente não linear, quando não podem ser linearizados (MAZUCHELI e ACHCAR, 2002; KUMAR, 2007).
O inconveniente da transformação é que, além do parâmetro perder sua interpretação intrínseca, pode-se alterar a estrutura e distribuição do erro, ou seja, se os erros do modelo original satisfazem as suposições usuais de normalidade, independência e homogeneidade da variância, os erros do novo modelo, em geral, não satisfazem tais suposições (MAZUCHELI e ACHCAR, 2002).
O uso de várias funções erros na definição da função objetivo tem como vantagem aumentar a chance de se encontrar um mínimo global. O estudo de simulação pode ser utilizado para verificar se o mínimo encontrado é um mínimo global estimado através da função erro normalizado. No modelo linear a adequação do modelo pode ser verificada pelo coeficiente de determinação (WILLWTT e SINGER, 1988), comparação do teste t com o valor (SHEWART e WILKS, 2006) e análise de variância.
O objetivo deste estudo foi utilizar o Origin e Excel para estimar os parâmetros de quatro modelos de isoterma de adsorção (Langmuir, Freundlich, Redlich-Peterson e Temkin) e cinco funções erros (soma do quadrado dos erros, função erro fracionário hibrido, desvio padrão percentual de Marquardt, erro Relativo médio e soma do erro absoluto) diferentes foram examinados e em cada caso os parâmetros foram determinados por minimização das funções erros.
MATERIAL E MÉTODOS: Foram estudados os modelos de Langmuir, Freundlich, Temkin, and Redlich-Peterson e cinco funções erros diferentes foram examinadas: Soma dos quadrados dos erros (ERRSQ), Função erro fracionário hibrido (HYBRD), Desvio padrão percentual de Marquardt (MPSD), Erro Relativo médio (ARE), Soma do erro absoluto (EABS) e em cada caso os parâmetros foram determinados por minimização das funções erros (Soma normalizada dos Erros – SNE) usando planilhas do Microsoft Excel (HO et al., 2002; ALLEN et al., 2003).
Para ilustrar a aplicação do Solver, segue abaixo o passo a passo para configurar os dados no Excel: Habilita-se a ferramenta solver no Excel; Destina-se na planilha uma célula para cada parâmetro da isoterma escolhida. Por exemplo, para o modelo de Langmuir, escolhe-se uma célula para receber o valor de KL e outra para receber o valor de qmax, escolhe um valor inicial para ambas variáveis. Estas células serão as células variáveis mencionadas anteriormente; Destina-se também células para o cálculo das funções erro, células de destino, a fim de encontrar o valor mínimo de cada uma destas funções; Seleciona-se o Solver para otimizar os dados, preenchendo na janela os parâmetros do solver: célula de destino (função erro), células variáveis (qmáx e KL).
No Origin: Inicia-se o programa, digitando os dados e depois selecionando-os; Seleciona-se no menu Analysis a opção nonlinear curve fit, Seleciona-se o menu função; Configura-se os dados de acordo com o modelo de isoterma; Foram escolhidos como valores iniciais q=1, k=1, para posterior comparação com o software Microsoft Excel; Foram colocadas as condições de contorno para os parâmetros a serem estimados, q<=40, K<=1, parâmetros obtidos a partir da análise de regressão linear, clicar o botão FIT.
RESULTADOS E DISCUSSÃO: A função erro utilizada no Origin, ERSSQ, também foi usada no Excel retornando os mesmos valores de parâmetros estimados. Como no Excel foi realizada a normalização dos erros foi possível obter menor erro associado à regressão e através de análise de variância não foi possível notar diferença significativa, Fcalc=0,015<Fcrít=2,089, ao nível de significância de 0,05 entre os modelos com parâmetros estimados pelo Origin e pelo Excel.
A função erro HYBRID retornou o menor valor do erro normalizado (SNE) utilizando o EXCEL para todos os modelos de isoterma de adsorção com exceção do modelo de Redlich-Peterson, o qual a função erro MPSD obteve menor valor normalizado (Tabela 1). O modelo de Redlich-Peterson melhor representou os dados experimentais, tanto pelo Excel quanto pelo Origin (Figura 1), mas quando se compara os valores do expoente β estimado pelas duas equações, verificou-se que o valor de β estimado pelo Origin se aproxima de 1, tornando-se semelhante a equação de Langmuir, fato que pode ser comprovado pelos valores próximos de Qmax de Langmuir e Q de Redlich-Peterson, diferente dos valores de Qmáx e Q estimados pelo Excel, os quais diferem entre si.
Tabela 1

Parâmetros dos modelos de isotermas de adsorção estimado pelo EXCEL
Figura 1
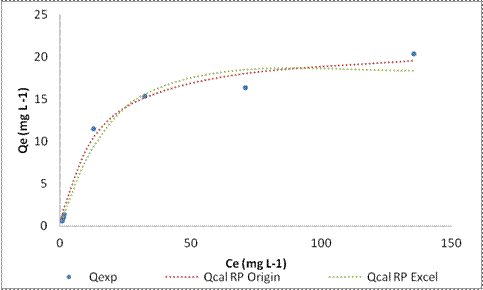
Comparativo da isoterma de Redlich-Peterson estimada pelo Origin e pelo Excel.
CONCLUSÕES: O EXCEL é uma ferramenta útil na estimação de parâmetros de isotermas de adsorção, não havendo diferença significativa quando comparado com o software Origin. O EXCEL possui a vantagem da configuração de várias funções erro em busca do mínimo global. O modelo de Redlich-Peterson melhor representou os dados experimentais, tanto pelo Excel quanto pelo Origin. Para todos os modelos de isoterma de adsorção, a função erro HYBRID foi a que obteve o menor erro normalizado, em conseqüência a melhor estimativa dos parâmetros, com exceção de Redlich-Peterson, o qual a função erro MPSD obteve menor valor
AGRADECIMENTOS:
REFERÊNCIAS BIBLIOGRÁFICA: ALLEN, S. J.; GAN, Q.; Matthews, R.; Johnson, P. A. Comparison of optimised isotherm models for basic dye adsorption by kudzu. Bioresour. Tech. V., p. 143-152, 2003.
HO, Y. S.; PORTER, J. F.; MCKAY, G. Equilibrium Isotherm Studies For The Sorption Of Divalent Metal Ions Onto Peat: Copper, Nickel And Lead Single Component Systems. Water, Air, and Soil Pollut. V. 141, p. 1–33, 2002.
KUMAR, K. V. Optimum sorption isotherm by linear and non-linear methods for malachite green onto lemon peel. Dyes Pig. V. 74, p. 595-597, 2007.
MAZUCHELLI, J.; ACHCAR, J. A. Algumas considerações em regressão não linear. Maringá , V. 24, p. 1761-1770, 2002.
SEBER, G. A.; WILD, C. J. Nonlinear Regression. New Jersey: John Willey & Sons, 2003.
SHEWHART, W. A.; WILKS, S. S. Regression Analysis by Example. 4. th ed. New York: Wiley Interscience, 2006.
WILLETT, J. B.; SINGER, J. D. Another Cautionary Note About R²: Its Use in Weighted Least Square Regression Analysis. The American Statistician , v. 42, p. 236-238, 1988.
