52º CBQ - Aplicação do Método de Monte Carlo para o estudo das Reações Químicas do Tipo A↔B→C

ÁREA: Físico-Química

TÍTULO: Aplicação do Método de Monte Carlo para o estudo das Reações Químicas do Tipo A↔B→C

AUTORES: Rodrigues Farias, R. (UESB) ; Matos de Oliveira Neto, N. (UESB) ; Martins Cardoso, L.A. (UESB) ; Santos Brito da Silva, G. (UESB)

RESUMO: Neste trabalho investigamos características de dinâmica das reações químicas homogêneas e elementares do tipo A↔B→C. A abordagem é realizada via Método de Monte Carlo cuja dinâmica considera as barreiras energéticas de cada etapa da reação, bem como a temperatura. O modelo proposto imita o comportamento usual das reações químicas aqui tratadas quanto sua dependência com a temperatura e energias de ativações de cada etapa da reação. Neste sentido, o modelo proposto pode servir com um efetivo laboratório para o ensino e pesquisa em Físico-Química.

PALAVRAS CHAVES: Reações Químicas; Monte Carlo; Cinética Química

INTRODUÇÃO: Os métodos de Química Teórica estão sendo largamente utilizados para estudar propriedades de sistemas físicos e químicos (FREITAS et al., 1999). O desenvolvimento destes estudos tem como finalidade propor modelos para simular um sistema real. Tais modelos, em linguagem matemática, são expressos por equações integrais e diferenciais, nos quais as soluções por métodos analíticos não são fáceis de resolver. Os experimentos computacionais têm um papel importante na ciência contemporânea por ser uma terceira via na abordagem de problemas, tão importante quanto às previsões teóricas e os resultados experimentais (COUTINHO et al., 2000; BINDER et al., 1984). Devido à onipresença das reações químicas em nossas vidas e o impacto destas na sociedade moderna é natural que se busque cada vez mais entender os mecanismos fundamentais que confere aos sistemas que reagem quimicamente suas propriedades Físico-Químicas. Assim sendo, muitos esforços são realizados para o entendimento dos mecanismos básicos das reações químicas (DICKMAN et al., 1999; ZIFF et al., 1986). Neste trabalho, temos como objetivo utilizar uma técnica de simulação computacional conhecida como Método de Monte Carlo (MMC) para estudar reações químicas homogêneas e elementares do tipo A↔B→C, nesta investigação pretendemos observar os comportamentos usuais de tal tipo de reação com relação aos parâmetros chaves em questão: temperatura e energias de ativações de cada etapa da reação global. Além disso, pretendemos desenvolver uma compreensão mais adequada do uso do MMC e sua aplicação/potencialidade no tratamento de sistemas químicos complexos.

MATERIAL E MÉTODOS: No método proposto, o sistema possui um número N de moléculas do tipo A, B e C, tal que N=NA+NB+NC seja constante. Utilizando o Método de Monte Carlo definimos as probabilidades de transição entre cada etapa da reação da seguinte forma (FARIAS et al., 2011): PAB=exp(-EA/KBT) PBA=exp(-EA/KBT) PBC=exp(-EA/KBT) onde KB é a constante de Boltzmann, T a temperatura, e EA, EB e EC as barreiras energéticas que devem ser superadas por uma dada molécula para que uma etapa da reação A→B, A←B e B→C ocorra. Por simplicidade, definimos os parâmetros Ө=KBT/EA com a temperatura medida em relação à energia de ativação EA, EBA=EB/EA e ECA=EC/EA as energias de ativação EB e EC medidas com relação a EA. A condição inicial utilizada é todas as moléculas na forma A, i.e., NA=N, NB=NC=0 (LOPEZ- CASTILHO, 2007). Passos de Monte Carlo: (i) Tentamos selecionar aleatoriamente uma molécula do tipo A. Se não conseguimos, um número aleatório z uniformemente distribuído em [0,1] é gerado e comparado com PAB. Se z<PAB, A se transforma em B. Caso contrário A permanece em sua forma original. (ii) Tentamos selecionar aleatoriamente uma molécula do tipo B. Se não conseguimos, o passo finaliza. Se conseguirmos, um número aleatório z uniformemente distribuído em [0,1] é gerado. Se z<PBC então B se transforma em C; se não, um número aleatório z uniformemente distribuído em [0,1] é gerado e se z<PBA, B se transforma em A. Caso contrário B permanece em sua forma original. Executando os passos (i) e (ii) N vezes, sendo N número de moléculas totais, i.e., N=NA+NB+NC. Nos resultados utilizamos N=102 e uma média sobre 102 amostras, como também, analisamos o comportamento das concentrações de A, B e C em função do passo de MC (tempo).

RESULTADOS E DISCUSSÃO: Com o modelo matemático proposto realizamos simulações variando-se Ѳ, EBA e ECA e analisamos o comportamento dinâmico das concentrações do reagente A, do intermediário B e do produto C. Na Figura 1(a), exibimos os resultados das concentrações em função do tempo para Ө=1,0, EBA=0,5 e ECA=2,5. Observamos que a concentração do reagente A decresce com o tempo, enquanto o intermediário B é formado. Somente após a formação de B que o produto C é formado. Como era de se esperar a etapa inicial da reação global é a mais rápida, uma vez que, EC=5EB e EC =2.5EA, ou seja, a barreira energética para B se transformar em C, barreira da ultima etapa da reação, é maior do que aquela relacionada com a etapa inicial. Para estudar essa reação, com a etapa mais rápida sendo a última, simulamos nosso sistema com valores de EBA=0,5, mas com EC=0,15EA. Os resultados são plotados na Figura 1(b). O comportamento ideal é similar àquele exibido na Figura 1(a), exceto pelo fato de que à medida que o intermediário B é formado mais rapidamente, comparado com EC=2,5EA, se transformar no produto C (Todos os resultados de acordo com a literatura). Outro comportamento que podemos observar com este modelo, é aquele relacionado com a temperatura. Na Figura 2 exibimos resultados das simulações para os mesmos valores de EB e EC utilizados para gerar os resultados da Figura 1(a), porém aumentamos a temperatura para Ө=2,0. Como era de se esperar, o aumento da temperatura fez com que o reagente A decaia mais rapidamente e a reação global como todo seja acelerada.

Figura 1

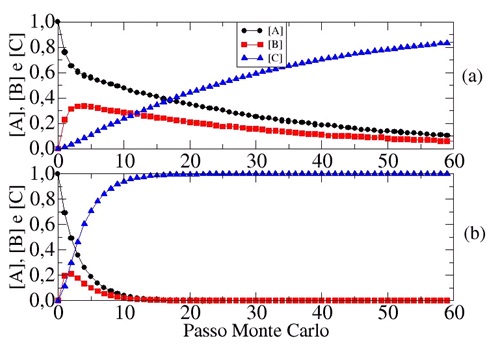
Concentração de A, B e C versus Passo de Monte Carlo (tempo), tanto para Figura (a) quanto para (b)

Figura 2

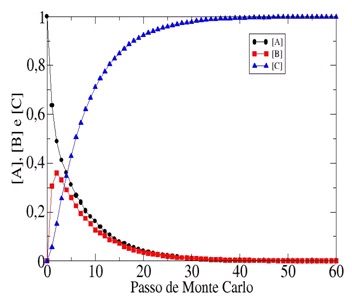
O comportamento dinâmico da concentração de A, B e C em função do Passo de Monte Carlo (tempo) para Ө=2,0, EBA=0,5 e ECA=2,5

CONCLUSÕES: Neste trabalho modelamos e simulamos reações homogêneas e elementares do tipo A↔B→C. Os resultados obtidos nas simulações estão de acordo com aqueles observados nestes tipos de reações químicas, validando assim, o modelo aqui proposto. Por fim, ressaltamos que o modelo aqui proposto, é mais adequado para o estudo destes tipos de reação de que aquele apresentado por López-Castilho (2007), uma vez que o mesmo inclui as energias de ativação e a temperatura como parâmetros chaves.

AGRADECIMENTOS: Os autores agradecem a UESB, CAPES e CNPq, pelo apoio e incentivo.

REFERÊNCIAS BIBLIOGRÁFICA: A. G. DICKMAN, B. C. S. GRANDI, W. FIGUEIREDO, and R. DICKMAN, Phys. Rev. E 59 6, 6361-6369 (1999).
A.LÓPEZ-CASTILHO, J. C. DE SOUZA FILHO. Simulação do Equilíbrio: o Método de Monte Carlo, Quim. Nova, vol. 30, (2007) 1759-1762.
BARLETTE, V.E. & FREITAS, L.C.G. “Termodinâmica Estatística de Líquidos com o Método de Monte Carlo. I. Metodologia” Quim. Nova, 22(2): 254, (1999).
BINDER, K., HEERMAN, D. W. Aplications of the Monte Carlo methods in statistical phisics, Springer-Verlag Berlin Heidelberg (1984).
K. COUTINHO, “Método Monte Carlo Aplicado a Simulação de Líquidos”, no Livro de Resumos da VII Escola Brasileira de Estrutura Eletrônica, pp. 48-73, (2000).
R. M. Ziff, E. GULARI, and Y. BARSHAD, Phys. Rev. Lett. 56 2553 (1986).
R. R. FARIAS, L. A. M. CARDOSO, N. M. OLIVEIRA-NETO, Exatas Online, v.2 n.2 7-13 (2011).